[科普中国]-惠勒-得卫特方程-

在理论物理中，惠勒-得卫特方程（英语：Wheeler-DeWitt equation，简称惠-德方程）是一个描述宇宙波函数必须满足量子引力理论的方程。

简介在理论物理中，惠勒-德维特方程（英语：Wheeler-DeWitt equation，简称惠-德方程）是一个描述宇宙波函数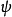必须满足量子引力理论的方程。其中一个波函数的例子是哈妥-霍金态。

简单说，惠-德方程的数学形式为：

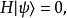其中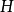是量子化广义相对论中的全部哈密顿约束。广义来说，在一个时间尺度不变性的理论中，哈密顿算符会是零。

虽然符号上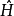，与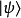和传统非相对论性量子力学所用符号相同，然而诠释上，惠勒-德维特方程则与非相对论性量子力学中的方程大相径庭。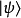不再是传统上空间波函数的观点(即一复数值的函数，定义于3维类空表面，且归一化。相对地，它是个定义于时空整体的场结构的泛函。此项波函数包含了所有关于宇宙几何以及物质内涵的所有信息。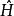依然是作用在希尔伯特空间中各个波函数上的一项算符，但是这个希尔伯特空间已与非相对论性量子力学中的希尔伯特空间不同，而且哈密顿算符不再决定系统的演化（所以薛定谔方程——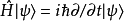——不再适用）。

此方程源自于ADM形式。1

ADM质量理论物理学中，以RichardArnowitt、StanleyDeser及查尔斯·米斯纳（Charles W.Misner）三人姓氏字首为名的ADM质量（ADM energy）或等价地称ADM能量是一个于广义相对论定义能量的特殊方法。此法只能应用到一些特别的时空几何，这些几何可以渐进式地接近一个在无限远处有良好定义的度规张量，举例来说：能渐进式地接近闵可夫斯基时空的一种时空几何。在这些例子中的ADM能量定义为此度规张量与其渐进接近的度规张量偏离程度之函数。换句话说，ADM能量是在无限远处重力场强度的计量。

这个量又称作“ADM哈密顿量”（ADM Hamiltonian），特别是存在有不同于上方定义但却仍可得到相同结果的公式。若要求的渐进形式是时间无关（例如闵可夫斯基时空本身），则涉及到时间平移对称性。诺特定理于是引出ADM能量是守恒的。根据广义相对论，在更一般性、时间相依的背景下，总能量守恒定律无法成立——举例来说，在物理宇宙学中，其即被完全违反。其中特别是宇宙暴胀可以从“无”中产生出能量（以及质量），因为真空能量密度大约是个常数，但宇宙总体积是以指数成长的速率在增加（膨胀宇宙）。2