[科普中国]-静力均衡

静力均衡是静力学的概念，常用于静力分析中。指大气中铅直方向的气压梯度力和重力的平衡。是静定结构受力分析的重要条件之一。

静定结构，一种类型的结构体系，指无多余约束的几何不变体系。其内力及支反力可由平衡条件完全确定，该结构的基本静力学特性是满足平衡条件内力解的惟一性，在此基础上派生出如下特性：1.温度变化、支座移动和制造误差等因素不引起该结构内力；2.结构的局部平衡性；3.结构的荷载等效性；4.结构的构造变换性。1

相关概念静力力学的一个部分，它研究物体在力的作用下处于平衡的规律，建立各种力系的平衡条件。静力学还研究力系的简化和物体受力的基本分析方法。物体受到几个力的作用，仍保持静止状态，或匀速直线运动状态，或绕轴匀速转动状态，叫做物体处于平衡状态，简称物体的平衡。处于平衡状态的物体，可以是静平衡，即物体既无平动，又无转动，保持静止，也可以是动平衡，即物体作匀速直线运动，或匀角速转动。无论是处于静平衡，还是动平衡，物体的受力情况是没有区别的。区别在于物体的初始状态，即物体开始处于力平衡的瞬时，它为静止的，还是平动或转动的。

静力学发展时期，是从公元前3世纪，到16世纪伽利略奠定动力学基础为止。阿基米德是使静力学成为一门真正科学的奠基者。著名的意大利艺术家、物理学家和工程师达·芬奇，对静力学的建立作出了重要贡献。静力学的基本物理量是力、力偶和力矩。学科内容主要包括以下几个方面：

①力作用于物体的效应分为外效应和内效应。外效应是指力使整个物体对外界参照系的运动变化; 内效应是指力使物体内各部分相互之间的变化。对刚体不必考虑内效应。

②静力学公理。静力学的全部推理是以几个简单公理为基础的。这些公理是人类在长期的生产实践中积累起来的力的知识的总结。它反映了作用在刚体上的力的最简单、最基本的属性，这些公理的正确性是可以通过实验来验证的，但不能用更基本的原理来证明。

公理Ⅰ： 二力平衡原理。

公理Ⅱ： 加减平衡力系原理。可在作用于刚体上的已知力系中增加一个平衡系，或者从这个力系中减去一个平衡系，而不改变原力系对刚体的作用效果。

公理Ⅲ： 力的平行四边形法则。

公理Ⅳ： 作用和反作用定律。

公理Ⅴ： 硬化原理。设一个变形体在一个力系作用下，处于平衡状态，若将这种状态下的变形体看成刚体，则其平衡状态不被破坏。

静力学知识在工程技术中有直接的应用。例如，对轴上零件的受力分析，从而合理地布置轴承;应用平衡条件求出轴承反力，作为选用轴承的一个依据; 对考虑摩擦力的平衡问题进行分析，得出某些零件的自锁条件，以便正确地设计这些零件等等。2

静力平衡大气中铅直方向的气压梯度力和重力的平衡。大气既有水平运动，也有垂直运动。一般情况下垂直运动的加速度比重力加速度小得多而可忽略，可认为每一薄层大气受到的重力与铅直方向的气体压力（气压梯度力）相平衡，即处于静力平衡状态。据此导出静力学关系：

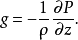
式中：g为重力加速度；ρ、P分别为空气密度和压强，z为高度。等式右边代表单位质量空气的气压梯度力。因为ρ总是正值，所以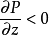，气压总是随高度递减。静力学关系在大气静止或匀速垂直运动时是完全正确的，在实际大气中，除去垂直运动强烈的积云环流外，它也能成立，故得到广泛应用。3

检查方式①将工作件置于均衡装置上，让其静止，注意位置。

②转动工作件约45°并放开，如有运动，即为工作件欠均衡。

③当静止时，利用塑像用粘土或磁性重量在工作件的最高点增加重量，此点与最重点成180°。

④转动工作件90°并放开。如工作件移动，必须调整所加的重量，如加重的部位停在底部，必须减轻重量；如加重的部位停在顶部，必须增加较多的重量。

⑤调整重量，直至工作件以不同的位置转动及放开时，均保持不动为止。

⑥确定使工作件均衡所加的实际重量。

⑦永久附加材料于工作件，或由最重点除去部分材料，并检查均衡。4

应用结构弹塑性地震反应分析方法，是通过建立结构的计算模型，依据结构构件的弹塑性恢复力特性，对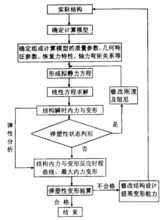结构进行地震作用下计算分析，从而获得结构的弹塑性反应。通过结构弹塑性地震反应分析，可以了解到结构各部位在地震作用下反应的全过程。因此，结构弹塑性地震反应分析方法对于评价和检验建筑结构的抗震性能有着十分重要的意义。结构弹塑性地震反应分析的基本流程如图1所示。做结构的弹塑性分析时，比较常用的方法有两种:静力荷载增量法和直接动力积分法。静力荷载增量法较简便，但地震作用是一种动力作用，要假设成为一个固定水平荷载，有很多问题和缺点。地震作用和建筑物本身的性能、振型变化有着密切的关系，建筑物在逐步进人塑性屈服时，建筑物的周期T、振型和阻尼比等都会发生变化，所以水平力的大小和分布状况都会发生变化，因此用一个固定的等值水平力来做静力分析，必然会带来计算上的误差。

结构弹塑性地震反应计算，应根据具体情况，如：结构组成、构件特点、计算机容量和计算费用等选用简化的计算模型。目前比较成熟和通用的有等效剪切型模型、平面杆系模型和空间弹塑性模型。等效剪切型模型是以结构层为计算单元，将每层中所有柱合并成一个总的层间抗剪构件来进行计算，这种模型能够快速、扼要地提供工程设计上所需的层剪力和层间位移，具有计算费用低等特点，但是，该模型无法对结构构件做仔细分析，无法考虑水平地震力引起的竖向荷载的变化对构件屈服的影响。平面杆系模型是由可带刚域的杆件组成的等效框架结构。计算中以框架每一杆件（包括梁、柱和墙）为基本构件（单元），该模型可精确求得结构各部位、各构件在地震作用下受力和变形的全过程。因此，应用该模型不仅可以求出地震过程中每一杆件是否开裂或屈服，还可以知道各杆件屈服的先后次序，从而了解整个结构的破坏形态。一般来说，当只需了解结构层剪力和层位移时，可采用层剪切模型；当需要了解塑性铰出现的确切位置及构件的破坏状态时，结构平面及立面布置均匀时可采用平面杆系模型。5

本词条内容贡献者为:

李雪梅 - 副教授 - 西南大学