[科普中国]-高斯-博内定理

在微分几何中，高斯-博内定理（亦称高斯-博内公式）是关于曲面的图形（由曲率表征）和拓扑（由欧拉示性数表征）间联系的一项重要表述。它是以卡尔·弗里德里希·高斯和皮埃尔·奥西安·博内命名的，前者发现了定理的一个版本但从未发表，后者1848年发表了该定理的一个特例。

定理内容设M是一个紧的二维黎曼流形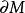， 是其边界。令K为M的高斯曲率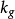， 为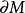 的测地曲率。则有

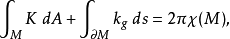其中dA是该曲面的面积元，ds是M边界的线元。此处 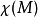是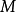 的欧拉示性数。

如果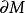 的边界是分段光滑的，我们将 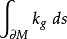视作光滑部分相应的积分之和，加上光滑部分在曲线边界上的转过的角度之和。1

一般化的高斯-博内定理广义高斯-博内定理(generalized Gauss–Bonnet theorem)成立于偶数维数的闭黎曼流形。在偶数维数的闭黎曼流形，欧拉示性数仍然可以表达为曲率多项式的积分。

公式：

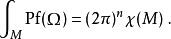
这是对于高维空间的直接推广。

例如在四维空间：

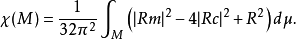
二维高斯-博内定理的操作式证明陈省身大师曾给出高维里高斯-博内定理的一个内蕴证明。用指南车也能给出二维高斯-博内定理的操作式证明。2

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学