[科普中国]-静水弯矩曲线

船体梁在静水中受到的剪力沿船长分布状况的曲线称为静水剪力曲线。是静水剪力曲线的一次积分，静水载荷曲线的二次积分。

静水载荷曲线由重力曲线、浮力曲线确定。

浮力曲线又由静水平衡经邦戎曲线求得。

简介船体梁1在静水中受到的剪力沿船长分布状况的曲线称为静水剪力曲线。

作用在船体梁任意剖面上的静水弯矩计算公式如下：

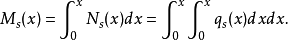
其中，Ms表示静水弯矩，Ns表示静水剪力，qs表示静水载荷。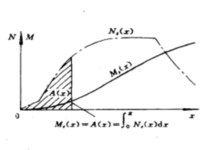

可见，静水载荷曲线的二次积分是静水弯矩曲线。其关系如图1。

由于船体两端是完全自由的，因此，首、尾端点处的剪力和弯矩应为零，亦即剪力和弯矩曲线在端点处是封闭的。

其次，由于载荷、剪力、弯矩之间有下列微分关系：

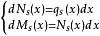
所以，零载荷点与剪力的极值相对应，零剪力点与弯矩的极值相对应。在大多数情况下，载荷在船中前和中后大致上是差不多的，所以剪力曲线大致是反对称的，零点在靠近船中的某处，而在离首、尾端约船长的1/4处具有最大正值或负值。此外，由于两端的剪力为零，即弯矩曲线在两端的斜率为零，所以弯矩曲线在两端与纵坐标轴相切。在计算过程，常常利用这些性质来检查计算结果是否正确。

载荷曲线载荷曲线2等于重力曲线纵坐标与浮力曲线纵坐标之差，用qs(x)表示，即qs(x)=p(x)-bs(x)。

重力曲线船舶在某一计算状态下，描述船舶所受重力沿整个船长分布状况的曲线，称为重力曲线。在手工计算中，常将船舶各项质量按静力等效原则分布到相应的20个理论站距内 ,作出近似的阶梯形质量分布曲线 ,并以此来代替真实的重力分布曲线。

浮力曲线船舶在某一装载情况下，描述浮力沿船长分布状况的曲线称为浮力曲线。浮力曲线通常由邦戎曲线、静水力曲线及船舶的质量质心等资料确定，其关键在于静水平衡的计算，即船舶在静水中艏艉吃水的确定。静水平衡的计算步骤如下。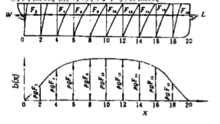

①从静水力曲线图中查出如下数据：平均吃水dm(m)，浮心距船中的距离xb（舯前为正，m），纵稳心半径R(m)，水线面面积A(m2)，漂心距船中的距离xf（舯前为正，m），重心距船中距离xg（舯前为正，m）。

②若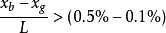，则可确定船舶纵倾后的第一次近似艏、艉吃水：

艏吃水——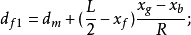

艉吃水——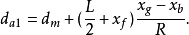

③若不能满足下面的精度要求，则应作第二次近似计算：

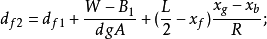
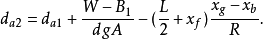
④一般说来，平衡计算一直要进行到达到下述要求，才能终止，即：

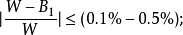
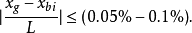
⑤静水平衡计算完毕后，就可利用邦戎曲线求得浮力曲线（见图2）。

应用实例通过以理论分析及对4,990吨级油船的具体计算及比较，得到以下结论：

①不同船舶、不同工况下的静水剪力、静力弯矩分布值及最大值相差较大，不同工况下的最大静水剪力、弯矩位置也略有不同，需要仔细计算；

②由于静水载荷、静水剪力、静水弯矩是积分关系，因此零载荷点与剪力的极值相对应；而艏、艉端点处的剪力与弯矩应为零；

③一般情况下，载荷在船中前和中后大致上是差不多的，所以剪力曲线大致是反对称的，弯矩最大值点在靠近船中的某处，而在离艏、艉端约船长的1/4处剪力具有最大正值或负值。1

本词条内容贡献者为:

张磊 - 副教授 - 西南大学