[科普中国]-相当平板

"相当平板"假定认为:实船或船模的摩擦阻力分别等于与其同速度、同长度、同湿表面积的光滑平板摩擦阻力。

概述"相当平板"假定认为:实船或船模的摩擦阻力分别等于与其同速度、同长度、同湿表面积的光滑平板摩擦阻力。这样，当已知船的水线长Lwl、航速VS及湿面积S，就可以利用平板摩擦阻力公式来计算船体摩擦阻力1。

尺度效应修正在应用实验方法研究船的快速性问题时，由于模型和实船（或实桨）之间的绝对尺度不同，且不能同时满足全相似定律，因而引起某些力、力矩或压力系数甚至流态等性能方面的差别，这种差别被称为尺度效应或者尺度作用。

显然应用相当平板假定计算船体摩擦阻力时，必须注意到船模和实船之间的尺度效应问题。因为与实船相比，船模的尺度较小，同时又为了满足傅汝德定律，所以其速度也较低，因而实船与船模的雷诺数是不同的，两者的摩擦阻力系数的差别称为摩擦阻力尺度效应。在实船-船模阻力换算过程中，考虑到这种差别称为“摩擦阻力修正”或“尺度效应修正”。

平板摩擦阻力系数计算公式虽然计算机的应用和数值计算均有很大的发展,但要求解像船体这样形状极为复杂的物体的边界层问题尚不能给出可供工程上实用的结果。因此.目前计算船体摩擦阻力仍不得不以光滑平板摩撤阻力系数公式为基础。本节先介绍光滑平板摩擦阻力系数计算公式,然后说明船体摩擦阻力计算的处理方法。

光滑平板层流摩擦阻力系数公式当平板界层内全为层流状态时，勃拉齐(IBlasius)早在1908年根据层流界层微分方程式给出了理论上的精确解为：

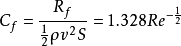此式称勃拉齐公式,与实验结果完全相符。必须说明的是,理论上得到的层流平板摩擦阻力系数的精确计算式,并不适用于造船工程实际,因其对应的雷诺数范围为: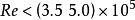。一般船舶的雷诺数在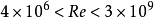,其对应的流动状态为紊流边界层。

1957ITTC公式1957年国际船模实验池会议实船-船模换算公式（简称1957ITTC公式）。在此之前已有的各光滑平板摩擦阻力公式的计算结果虽然很接近，但还有一定的差别。尤其在吧船模实验结果换算到实船时，由于应用公式不同，计算所得的实船阻力均存在不同程度的差别。为此1957年在西班牙马德里召开的第八届国际船模实验池会议（简称ITTC）上根据分析几何相似船模阻力的实验结果，认为桑海公式在低雷诺数时所得的数值偏低。最后提出下列新公式，叫做“1957年国际船模实验池会议实船-船模换算公式”，（简称1957ITTC公式）：

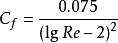
应该指出，1957ITTC公式并不完全是紊流光滑平板摩擦阻力系数公式，它专用于船模和实船的阻力换算。我国现用ITTC公式。

过渡流平板摩擦阻力系数公式根据边界层理论知,界层内的流动状态取决于雷诺数,靠近平板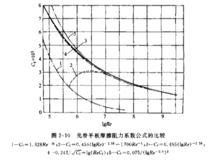前端,局部雷诺数比较小,所以产生层流。随着局部雷诺数的增高.则产生过渡流,直到最后完全呈紊流状态。所以,在平板边界层内三种流动情况都存在着。若平板的雷诺数较大,则紊流部分很大,基本上是紊流阻力,前端的层流和过渡流对整个平板的阻力影响较小。反之,Re较小时,前端层流和过渡流占整个平板界层的较大部分,以致对整个平板的平均阻力产生明显影响。

过渡流平板摩擦阻力系数可按柏兰特所给出的半经验公式计算:

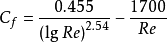
式中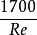为层流影响修正值。显见当Re很大时，该值趋于零，上式即成为柏兰特-许立汀公式。这说明平板界层内紊流占绝对主要部分，所以可以按全部紊流平板公式计算。

本词条内容贡献者为:

李雪梅 - 副教授 - 西南大学