正合三角形(exact triangle)是将正合列形象表示成的一种三角形,正合偶是由两个双分次模所组成的正合三角形。
基本介绍设M,N,K是三个左R-双分次模,并设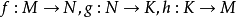 分别是
分别是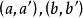 及
及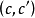 双次映射,若
双次映射,若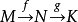 在N处正合,
在N处正合,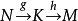 在K处正合,
在K处正合,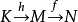 在M处正合,则称图
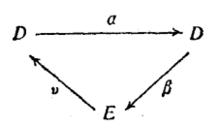
在M处正合,则称图
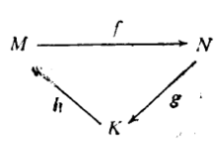
在每一个顶点处正合,并称此三角形是正合三角形。
相关概念正合偶正合偶(exact couple)是由两个双分次模所组成的正合三角形,它是马西(W.S.Massey)提出的,是谱序列理论一个重要概念。由正合偶可得出其导出偶,且由此可得出谱序列。若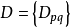 与
与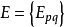 为两个双分次模,
为两个双分次模,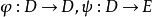 与
与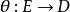 是分次模映射,依次有次数
是分次模映射,依次有次数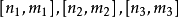 ,使在下列三角形的每个顶点处都正合,
,使在下列三角形的每个顶点处都正合,
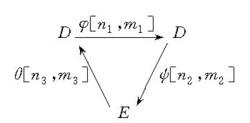
亦即有长正合序列:
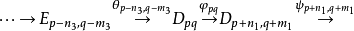
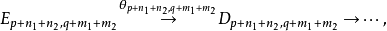 则称
则称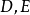 连同
连同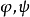 与
与 组成一个正合偶,记为
组成一个正合偶,记为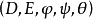 ,由正合偶可得出其导出偶,且由此可得出谱序列。1
,由正合偶可得出其导出偶,且由此可得出谱序列。1
我们可以利用函子来作正合偶,即有下面定理。
定理1设已给两个加法共变函子
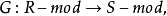
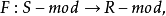 且满足:
且满足:
(i)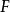 是左正合的;
是左正合的;
(ii) 当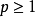 时,
时, ,
,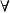 内射左
内射左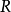 一模
一模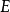 。
。
若A是左R-模,我们取定A的一个内射分解
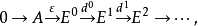 并记
并记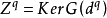 。
。
命:
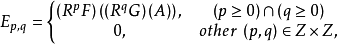
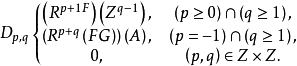 则存在双次数分别是
则存在双次数分别是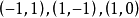 的双次映射
的双次映射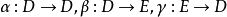 使
使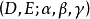 是一个正合偶,也即有正合三角形2
是一个正合偶,也即有正合三角形2
双分次模双分次模(bigraded module)是分次模概念的推广,指一些双指标的A模所组成的序列。若M={Mpq|p,q∈Z}是由A模Mpq所组成的序列,Z是整数集,称M={Mpq|p,q∈Z}为一个双分次模或称为双次模。若N={Npq|p,q∈Z}也是一个双分次模,m与n为一对整数,则模同态fpq:Mpq→Np+m,q+n的集合f={fpq|p,q∈Z}称为由M到N的[m,n]次的分次模映射。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国