一阶微分形式不变性是指:无论u,v是自变量还是中间变量,函数z=f(u,v)的全微分形式是一样的。此性质的好处是:一方面是可以不用区分变量直接利用一元函数的微分性质计算;另一方面是不用区分变量是自变量、因变量还是中间变量,以及它们的结构问题就可以利用微分性质直接计算。
定义若以 和
和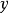 为自变量的函数
为自变量的函数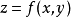 可微,则其全微分为
可微,则其全微分为
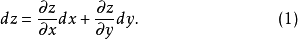 如果
如果 ,
,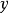 作为中间变量又是自变量
作为中间变量又是自变量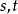 的可微函数
的可微函数
 由于复合函数
由于复合函数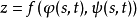 是可微的,其全微分为
是可微的,其全微分为
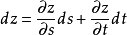
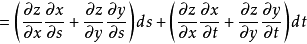
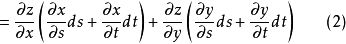
由于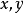 又是
又是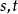 的可微函数,因此同时有
的可微函数,因此同时有
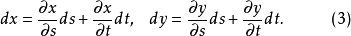
将(3)式代入(2)式,得到与(1)式完全相同的结果。这就是关于多元函数的一阶(全)微分形式不变性1。
这是一阶全微分的一个非常重要的性质,有了这个“形式不变性”作保证,对于一个函数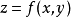 就可以按照
就可以按照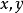 是自变量去求它的微分
是自变量去求它的微分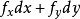 ,而无需顾忌
,而无需顾忌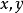 究竟真的是自变量,还是一个随自变量
究竟真的是自变量,还是一个随自变量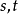 变化的中间变量。
变化的中间变量。
在微积分的教与学的过程中,利用这个性质求解较复杂的多元函数特别是复合函数,隐函数的偏导数,实用方便,简单易行。
在隐函数求导中的应用隐函数存在定理是微积分中的难点,一般的教材介绍这一部分时,尽管对定理的证明不做要求,但是推导偏导数的过程复杂,公式繁多,导致许多学生在求隐函数的偏导数时,常会出错,但若利用一阶微分的形式不变性对方程两边同时求微分,则可减少此类错误。
隐函数存在定理1设函数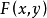 在点
在点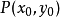 的某一领域内具有连续的偏导数,且
的某一领域内具有连续的偏导数,且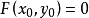 ,
,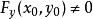 。则方程
。则方程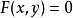 在点
在点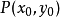 的某一领域内恒能惟一确定一个单值连续且具有连续偏导数的函数
的某一领域内恒能惟一确定一个单值连续且具有连续偏导数的函数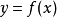 ,它满足条件
,它满足条件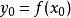 ,并有2
,并有2
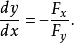 证明 设函数
证明 设函数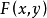 在点
在点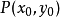 的某一领域内具有连续的偏导数,且
的某一领域内具有连续的偏导数,且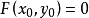 ,则函数可微。于是
,则函数可微。于是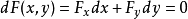 。由于
。由于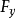 连续,且
连续,且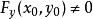 ,由连续函数的保号性,存在
,由连续函数的保号性,存在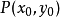 的某一领域,在该领域内,
的某一领域,在该领域内,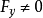 。于是可得结论成立。
。于是可得结论成立。
隐函数存在定理2设函数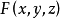 在点
在点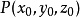 的某一领域内具有连续的偏导数,且
的某一领域内具有连续的偏导数,且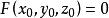 ,
,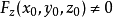 。则方程
。则方程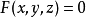 在点
在点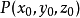 的某一领域内恒能惟一确定一个单值连续且具有连续偏导数的函数
的某一领域内恒能惟一确定一个单值连续且具有连续偏导数的函数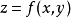 ,它满足条件
,它满足条件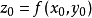 ,并有2
,并有2
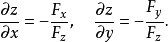 证明 设函数
证明 设函数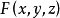 在点
在点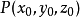 的某一领域内具有连续的偏导数,且
的某一领域内具有连续的偏导数,且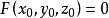 ,则函数可微。于是
,则函数可微。于是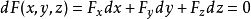 。由于
。由于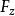 连续,且
连续,且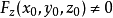 ,由连续函数的保号性,存在
,由连续函数的保号性,存在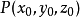 的某一领域,在该领域内,
的某一领域,在该领域内,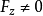 。于是得
。于是得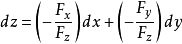 ,由一阶全微分形式不变性,可知结论成立。
,由一阶全微分形式不变性,可知结论成立。
隐函数存在定理3设函数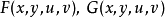 在点
在点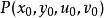 的某一领域内有对各个变量的连续偏导数,且
的某一领域内有对各个变量的连续偏导数,且 ,
,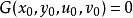 ,且偏导数所组成的函数行列式(或雅克比行列式)
,且偏导数所组成的函数行列式(或雅克比行列式)
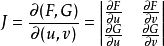 在点
在点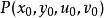 不等于零,则方程组
不等于零,则方程组 ,
,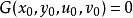 在点
在点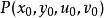 的某一领域内能惟一确定一组单值连续且具有连续偏导数的函数
的某一领域内能惟一确定一组单值连续且具有连续偏导数的函数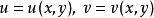 ,它们满足条件
,它们满足条件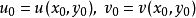 ,并有2
,并有2
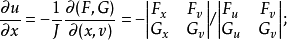
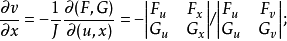
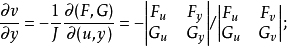
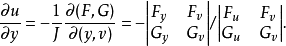 证明 设函数
证明 设函数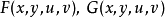 在点
在点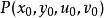 的某一领域内具有连续的偏导数,则函数可微。于是
的某一领域内具有连续的偏导数,则函数可微。于是
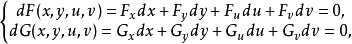
当偏导数所组成的函数行列式(或雅克比行列式)
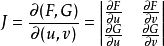 在点
在点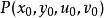 不等于零时,由连续函数的保号性,存在
不等于零时,由连续函数的保号性,存在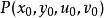 的某一领域内
的某一领域内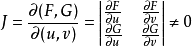 ,于是由Gramer法则得
,于是由Gramer法则得
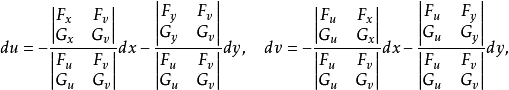 由一阶全微分形式不变性可得结论成立。
由一阶全微分形式不变性可得结论成立。
在复合函数求偏导中的应用复合函数的中间变量均为一元函数的情形设函数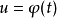 及
及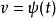 都在点
都在点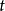 可导,函数
可导,函数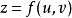 在对应点
在对应点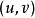 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数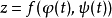 在对应点
在对应点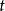 可导,且其导数可用下列公式计算2:
可导,且其导数可用下列公式计算2:
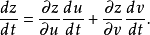 证明
证明 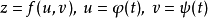 都可微,因此,由一阶微分形式不变性可得
都可微,因此,由一阶微分形式不变性可得
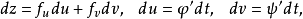 从而
从而
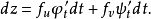 所以上述结论成立。
所以上述结论成立。
复合函数的中间变量均为多元函数的情形设函数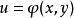 及
及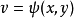 都在点
都在点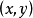 可导,函数
可导,函数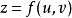 在对应点
在对应点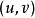 具有连续偏导数,则复合函数
具有连续偏导数,则复合函数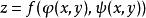 在对应点
在对应点 可导,且其导数可用下列公式计算2:
可导,且其导数可用下列公式计算2:
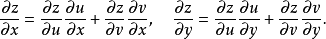 证明
证明 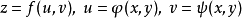 都可微,因此,由一阶微分形式不变性可得
都可微,因此,由一阶微分形式不变性可得
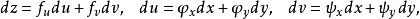 从而
从而
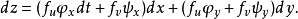 所以上述结论成立。
所以上述结论成立。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国