[科普中国]-全微分表达式

如果函数z=f(x, y) 在(x, y)处的全增量

Δz=f(x+Δx,y+Δy)-f(x,y)

可以表示为

Δz=AΔx+BΔy+o(ρ)，

其中A、B不依赖于Δx, Δy，仅与x,y有关，ρ趋近于0(ρ=√[(Δx)2+(Δy)2])，此时称函数z=f(x, y)在点（x，y）处可微分，AΔx+BΔy称为函数z=f(x, y)在点(x, y)处的全微分，记为dz即

dz=AΔx +BΔy

该表达式称为函数z=f(x, y) 在(x, y)处(关于Δx, Δy)的全微分的表达式。

简介编辑

为了引进全微分的定义，先来介绍全增量。

全增量设二元函数z = f (x, y)在点P(x,y)的某邻域内有定义，当变量x、y点(x,y)处分别有增量Δx，Δy时函数取得的增量。

称为 f (x, y)在点(x,y)的全增量。

全微分如果函数z = f (x, y)在点(x,y)的全增量

可表示为

其中A 、B仅与x、y 有关，而不依赖于Δx 、Δy，

，则称函数z = f (x, y)在点(x,y)处可微分，

称为函数z = f (x, y)在点(x,y)处的全微分。记作dz，即

。

函数若在某平面区域D内处处可微时，则称这个函数是D内的可微函数，全微分的定义可推广到三元及三元以上函数。[1-2]

定理编辑

定理1如果函数z=f（x，y）在点p0（x0，y0）处可微，则z=f（x，y）在p0（x0，y0)处连续，且各个偏导数存在，并且有f′x（x0，y0）=A，f′y（x0，y0）=B。

定理2若函数z=f（x，y）在点p0（x0，y0）处的偏导数f′x，f′y连续，则函数f在点p0处可微。

定理3若函数z = f (x, y)在点(x, y)可微分，则该函数在点(x,y)的偏导数

必存在，且函数z = f (x, y)在点(x,y)的全微分为：

判别可微的方法编辑

(1)若f (x,y)在点(x0, y0)不连续，或偏导不存在，则必不可微；

(2)若f (x,y)在点(x0, y0)的邻域内偏导存在且连续必可微；

(3)检查

是否为

的高阶无穷小，若是则可微，否则不可微1。[3]

极限、连续、可导、可微的关系编辑

这几个概念之间的关系可以用下图表示：

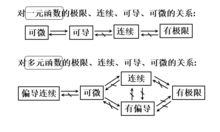
本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学