[科普中国]-质量－弹簧－阻尼器系统

质量－弹簧－阻尼器系统可用简单的数学模型表示，即数轴建模法，建立与系统平行方向的数轴，把弹簧或阻尼器的实际位移值当做有理数标在数轴上对应位置，然后按照有理数比较大小的结果确定相应质量块所受弹簧力或阻尼力的大小和方向，进而求得系统的微分方程。分别以单自由度系统、两自由度振动系统及多自由度系统为例，阐述了数轴法在建立机械振动系统的数学模型中的应用。结果表明此方法在列写质量－弹簧－阻尼器系统的运动微分方程时非常有效。

概念质量－弹簧－阻尼器系统是一种比较普遍的机械振动系统，研究这种系统对于我们的生活和科技也是具有意义的，生活中随处可见这种系统，例如汽车缓冲器就是一种可以耗减运动能量的装置，是保证驾驶员行车安全的必备装置。再者在建筑抗震加固措施中引入阻尼器，改变结构的自振特性，增加结构阻尼，吸收地震能量，降低地震作用对建筑物的影响。因此研究质量－弹簧－阻尼器系统很具有现实意义。

数学模型的建立研究背景数学模型是定量地描述系统的动态特性，揭示系统的结构、参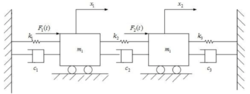数与动态特性之间关系的数学表达式。其中，微分方程是基本的数学模型，不论是机械的、液压的、电气的或热力学的系统等都可以用微分方程来描述。微分方程的解就是系统在输入条件下的输出相应。所以，建立数学模型是研究系统、预测其动态响应的前提。通常情况下，机械振动系统的微分方程都是应用力学中的牛顿定律、质量守恒定律等。

分析这种系统时，首先要根据弹簧、阻尼器的物理意义对与其固连的质量块进行受力分析，然后用牛顿第
二定律列写质量块对应的合力方程，从而得到系统的数学模型——微分方程。在对质量块进行受力分析时一般遵循这样的原则：

（1）弹簧受到外作用时，在线性范围内，弹簧力的大小与弹簧的形变成正比，弹簧力的方向总是与形变方向相反；

（2）尼器可以看作是一个活塞液压缸系统，当活塞和液压缸之间存在相对运动时，主动一方总要受到另一方的阻尼力。对于线性阻尼器，阻尼力的大小与阻尼器端点的相对移动速度成正比。外力作用下，当弹簧或阻尼器的两端点都产生位移时，在确定弹簧形变方向和阻尼器端点相对移动速度时，情况相对有点复杂。针对这一问题，研究提出了一种利用数轴建立弹簧一质量一阻尼系统的数学模型——微分方程的简单方法，称之为数轴建模法。

数轴建模法弹簧、阻尼器、质量块是组成振动系统的理想元件。在对实际机械结构进行振动分析时，有时可以略去阻尼，系统简化为质量一弹簧系统。当物理系统的质量很小时，系统就可近似成阻尼一弹簧环节。图1(a)所示即为阻尼～弹簧环节，已知弹簧的刚度为k，阻尼器的阻尼系数为c，输入为位移，系统在输入位移作用下的输出设为以。来看一下如何用数轴法分析系统受力情况，进而列写系统的微分方程。

假设系统的A点处存在一个质量块mA，这样可以通过分析其受力情况求得系统的微分方程。由于弹簧和阻尼器都是垂直放置的，故建立一竖直数轴。先来看数轴的正方向朝下的情况。将弹簧和阻尼器端点的位移顺序地标在数轴上对应位置，如图1(b)所示。弹簧在一端受到输入位移，作用后，另一端点也有位移，属于两端都产生位移的情况；阻尼器一端固定，另一个端点有位移输出。

如果按照一般的物理方法来列写系统微分方程，也需要取质量块mA为脱离体，对其进行受力分析。经过能量
损耗后，输出位移必定小于输入位移，故弹簧受压，所受弹簧力向下；质量块受到弹簧压力使得阻尼器的活塞杆向下移动，这样活塞杆将受到缸体施加的向上的阻尼力，此阻尼力传到质量块，故mA的受力分析简图如图1(e)所示。可见按照数轴法和一般物理方法求得的系统微分方程是一致的。

从上例可以看出，用数轴法分析系统受力，列写弹簧一质量一阻尼系统微分方程时，我们无需考虑弹簧的压缩或拉伸情况，也不用分析阻尼器内部活塞和液压缸的相互运动情况，只需建立一个数轴，规定原点、正方向和单位长度，把弹簧或阻尼器的输入位移变量和输出位移变量当作有理数按照实际顺序标在数轴上对应位置。

而弹簧力或阻尼力的方向的确定遵循以下原则：当系统中弹簧两端或阻尼器两端都有位移时，弹簧力或阻尼力的方向与所建立的数轴正方向相反；当弹簧或阻尼器只有一端有位移时，弹簧力或阻尼力的方向与弹簧或阻尼器端点的实际位移方向相反。

这种通过建立与系统平行方向的数轴，借助数轴分析系统中质量块的受力情况，进而根据牛顿第二定律列写系统微分方程的方法就称之为数轴建模法。在建立弹簧一质量一阻尼系统数学模型时，这种方法非常有效。

当弹簧一质量一阻尼系统含有两个或两个以上的质量块时，建立系统数学模型时需对每个质量块进行受力分析。由于相邻质量块间存在负载效应，用数轴法对系统进行受力分析时需考虑第一个进行受力分析的质量块如何选取。一般来说，前一个质量块的受力分析总是从相邻的后一个质量块受力分析开始。也就是说，第刀个质量块的受力分析要先考虑第n+1个质量块对其的作用。因此，可采取这样一个方法，即：沿着输入量(力或位移)作用方向寻找最后一个质量块，按照数轴法先分析其受力情况，然后逆实际运动方向依次分析其余质量块的受力情况，进而按照牛顿第二定律列出每个质量块的受力方程，然后联立即可得到系统的运动微分方程。

研究结论数轴建模法是一种简单有效的建立弹簧一质量一阻尼系统的数学模型的方法。它以数轴知识为基础，根据系统实际情况建立假想数轴，借助数轴确定系统中相应质量块所受弹簧力或阻尼力的大小和方向，进而求得系统微分方程。此方法在建立弹簧一质量一阻尼系统数学模型过程中起到了事半功倍的效果。1

高层钢结构调频液体阻尼器抗震控制优化设计研究背景调谐液体阻尼器是一种固定在结构楼层（或顶层）上的水箱。当结构在地震作用下而发生振动时，将带动水箱一起运动，使水箱中的水晃动起来产生波浪，此波浪对水箱壁的动水压力就构成了对结构的减振力。国内外对TLD用 于结构风振、地震反应控制研究较多。TLD用于结构抗风抗震控制已处于工程设计和实施阶段。面向工程设计，对TLD系统参数取值及简化设计进行研究，具有一定的应用前景。同时高层钢结构重量轻、阻尼系数小，所以更易采用结构振动控制技术，研究的主要目的旨在利用单个和多个调频液体阻尼器减小高层钢结构地震反应时的参数取值问题及高层钢结构-调频液体阻尼器系统抗震控制简化设计方法，将多个调频液体阻尼器系统的固有频率按线性分布进行设计即形成MTLD系统，研究其最优频带宽取值及高层钢结构-MTLD系统简化设计方法，为调频液体阻尼器的工程设计和实施提供参考。

TLD简化模型采用Housner质量-弹簧模型，引入液体阻尼，从而形成质量-弹簧-阻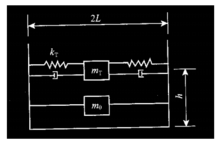尼器系统。设某一n层高层钢结构建筑，TLD系统设置于第k层，结构受基底地震加速度扰动输入，在地震作用下，水箱中的水将产生振动，箱壁产生的动液压力可分为脉动压力和振荡压力，脉动压力与水箱加速度成正比，但方向相反；振荡压力取决于液体振荡的波高和频率。两种动液压力可分别采用两个与箱体联接形式不同的等效质量的振荡效应来模拟。

研究结论（1）将单个和多个调频液体阻尼器引入高层钢结构抗震中，由于其装置简单、经济，因而具有一定的工程应用前景。

（2）研究根据“高层民用建筑钢结构技术规程”，对高层钢结构阻尼比取为0.02，对TLDs和MTLD的位置都假定设置于同一楼层。

（3）研究了单个和多个调频液体阻尼器设计参数，提供的设计参数可供工程设计查用，可以不考虑振型参与系数的影响；设计过程可为设计人员采用。

（4）数值分析及仿真分析表明，采用 目标函数设计的单个和多个调频液体阻尼器控制效果基本相同。

（5）采用目标函数设计的多个调频液体阻尼器，较采用目标函数，设计的多个调频液体阻尼器控制效果好；而且由于MTLD具有一定减震频带宽，所以MTLD较TLD/TLDs具有更好的鲁棒性。

（6）多振型控制时，可设置多个TLD/TLDs/MTLD系统，忽略振型间的相互作用，仿照本研究的设计思想与方法进行设计。2

本词条内容贡献者为:

王沛 - 副教授、副研究员 - 中国科学院工程热物理研究所