多元函数微分学是数学分析领域的重要内容。在多元函数微分学中,主要讨论的是多元函数的可微性及其应用,而二元函数的可微性则是多元函数可微性研究的重点。复合函数微分法则是二元函数可微性的进一步研究。
复合函数的求导法则设函数
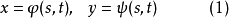 定义在
定义在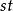 平面的区域
平面的区域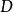 上,函数
上,函数
 定义在
定义在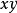 平面的区域
平面的区域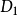 上,且
上,且
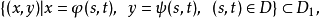 则函数
则函数
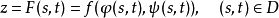 是以(2)为外函数,(1)为内函数的复合函数。其中
是以(2)为外函数,(1)为内函数的复合函数。其中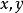 称为函数
称为函数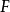 的中间变量,
的中间变量,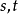 为
为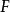 的自变量1。
的自变量1。
定理1若函数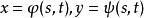 在点
在点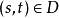 可微,
可微,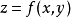 在点
在点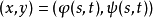 可微,则复合函数
可微,则复合函数
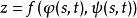 在点
在点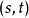 可微,且它关于
可微,且它关于 与
与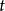 的偏导数分别为
的偏导数分别为
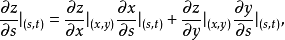
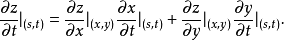
上述两个公式也称为链式法则。
注意如果只是求复合函数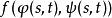 关于
关于 或
或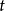 的偏导数,则定理1中
的偏导数,则定理1中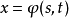 和
和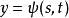 只需具有关于
只需具有关于 或
或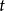 的偏导数就够了。但是对外函数
的偏导数就够了。但是对外函数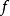 的可微性假设是不能省略的,否则上述复合函数求导公式不一定成立。如函数
的可微性假设是不能省略的,否则上述复合函数求导公式不一定成立。如函数
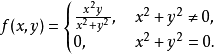
直接计算可知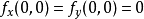 ,但
,但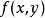 在
在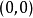 处不可微。若以
处不可微。若以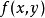 为外函数,
为外函数,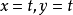 为内函数,则得以
为内函数,则得以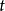 为自变量的复合函数
为自变量的复合函数
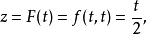 所以
所以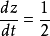 。这是若用链式法则,将得出错误的结果
。这是若用链式法则,将得出错误的结果
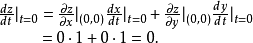 这个例子说明在使用复合函数求导公式时,必须注意外函数
这个例子说明在使用复合函数求导公式时,必须注意外函数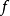 可微这一重要条件。
可微这一重要条件。
复合函数的全微分若以 和
和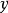 为自变量的函数
为自变量的函数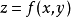 可微,则其全微分为
可微,则其全微分为
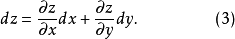 如果
如果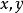 作为中间变量又是自变量
作为中间变量又是自变量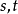 的可微函数
的可微函数
 则由定理1知道,复合函数
则由定理1知道,复合函数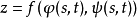 是可微的,其全微分为
是可微的,其全微分为
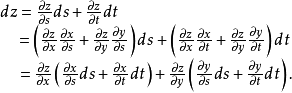
由于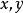 又是
又是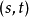 的可微函数,因此同时有
的可微函数,因此同时有
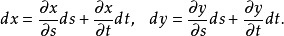
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国