[科普中国]-束流动力学

束流动力学在弯晶的束流控制技术得到了迅速发展.。在加速器物理中，粒子能量和束流强度一直是人们追求的目标，而引出技术和引出效率则是保证束流强度的关键。在束流动力学、经典力学框架内和偶极近似下，导出了粒子在弯晶中的一般运动方程。在准静态近似下，利用哈密顿原理分析了系统的稳定性；在相空间密度均匀分布假设下，利用相面积概念讨论了弯晶的引出效率。

概念束流动力学在现代加速器的发展中，是一个重要的研究方向。随着带电粒子束流强度的增大，束流内部的空间电荷力变得越来越重要了，而传统的利用几何模型处理空间电荷效应的方法无法提供所需要的精度。随着加速器束流动力学的深入发展和计算机运算能力的迅速提升，宏粒子准确模拟方法已成为研究加速器中带电粒子束行为特征的重要手段。在宏粒子模拟中，关键的技术是对空间电荷效应的准确计算。PP(Particle-Particle)方法和PIC(Particle-In-Cell) 是两种广泛采用的求解空间电荷效应的方法。PP方法中，每个宏粒子感受到的力由它与其余的每个宏粒子的力益加得到，这种方法计算量大，数据存储量大。在PIC方法中，先将所有宏粒子电荷分配到场网格节点上，然后求解 Poisson方程得到场网格节点上的场强，再利用插值的方法求得宏粒子感受到的空间电荷力。然后把空间电荷力盛加到外场力上，再对束流进行跟踪。PIC方法在强流束流动力学计算中有着广泛的应用。

750keV射频四极注入器束流动力学设计射频四极(RFQ)加速结构利用射频四极电场同时实现横向聚焦及纵向聚束与加速。RFQ 对离子的聚焦作用是通过射频四极电场实现的，适合于低能范围内(0.01～0.10 倍光速)对离子进行加速。RFQ可以以很高的效率捕获离子源出来的低能连续离子束，在较短的距离内加速到几百 keV 到几 MeV，同时把束流聚成束团。自1969 年苏联科学家 Kapchinsky 和 Tepliakov 提出RFQ 加速原理以来，RFQ 加速结构由于在低能离子加速方面独特的优越性，在世界范围内获得了广泛的应用。许多质子和重离子加速器都采用 RFQ 作为注入器或预注入器。我国近年来也在这方面开展了一定的研究。中国工程物理研究院将为35 MeV 质子直线加速器研制一台RFQ 加速器作为其注入器。

750 keV RFQ注入器系统的组成图1 给出了750 keV RFQ 注入器系统的主要组成部分。质子束从离子源出来后，经过低能传输段进入RFQ 加速器，经加速后，通过中能传输段注入到质子直线加速器中。图中射频功率源为 RFQ 加速器腔体和束流负载提供所需要的射频功率。

主要设计原则和技术要求设计中主要考虑以下几个方面的问题：(1)设计参数必须和 35 MeV 质子直线加速器的运行参数匹配。(2)所需的射频功率尽量小。这主要出于经济性的要求，因为射频功率源是整个系统最昂贵的部分，降低功率要求能显著降低造价。同时也能降低水冷系统的负载，提高加速器运行的可靠性。(3)电极表面最大场强适当。较小的场强使得加速效率降低，而较大的场强会增加加速器打火的概率。一般电极表面最大场强取值在1.8EK 左右，EK 为Kilpatrick 极限场强。(4)传输效率足够高。(5)尽可能减小各种非理想因素的影响。(6)对离子源流强、电压、发射度等参数的要求合理。一方面现有技术水平能实现，另一方面实现的代价不能太高。根据35 MeV质子直线加速器的运行参数等，提出了RFQ 加速器的主要技术要求，如表1所示。

750 keV RFQ加速器束流动力学设计采用经典的“四段论”RFQ结构，即把整个RFQ加速器分为径向匹配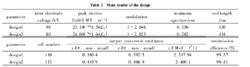段、成形段、慢聚束段和加速段四大部分。研究了两套设计方案，主要设计结果如表2所示。

图 2 给出了主要动力学参数沿纵向的分布。从图可见，主要动力学参数分布符合四段论的特征。图中a是最小孔径，m 是调制系数，B 是聚焦系数，φ是同步相位，W 是同步能量。

非理想匹配条件对束流传输效率的影响在加速器建造中，不可能达到各种条件均理想匹配，因此设计中分析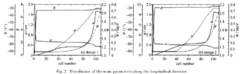了多种非理想匹配条件对传输效率的影响，包括能散、发射度、Twiss 参数、流强、能量。根据模拟结果，得到以下结论：

(1)当注入束流的能散在10%以内时，两套方案传输效率保持在 98%以上。因此两套方案对离子源的能散度要求均较低。

(2)当注入束流的横向归一化均方根发射度为 0.6 π·mm·m·rad，即设计值的3倍时，两套方案的传输效率都在 95%以上。这对于降低对离子源的要求，是很有利的。

(3)注入束流相椭圆的 Twiss 参数α和β在较宽的范围内变化，两套设计的传输效率都保持较高水平。例如取变化范围为设计值的40%时，传输效率基本在95%以上。因此设计对Twiss参数的变化不敏感，这对加速器建成后的调试是比较有利的。计算也发现，当相椭圆的β参数较小时，传输效率将明显下降，这种现象是可以理解的。因为β 较小时，束流的传输半径小，空间电荷效应更强，而空间电荷效应将引起束流横向和纵向的耦合振荡而造成粒子丢失。这一现象对于第 2 套设计方案更明显，因为其孔径较小，更容易在横向丢失粒子。

(4)传输效率随着注入流强的增加而下降是可以预期的，这仍然可以归结为空间电荷效应的影响。当注入流强达到设计值的2倍，即100 mA 时，两套方案的传输效率仍然保持在96%以上，这是令人满意的结果。

(5)当注入能量偏离设计值时，传输效率应下降。因为此时粒子能量偏离同步能量，纵向将产生强烈的相振荡，纵向相振荡通过空间电荷效应耦合到横向运动，从而造成粒子丢失。设计中当注入能量偏离设计值达到10%时，两套方案的传输效率仍然都高于92%。这对于加速器的调试以及降低对离子源的要求是很有利的。以上分析都针对单一参数，而实际情况中各个参数将同时作用，因此实际情况要复杂得多。本设计中两套方案对各种不匹配参数都有较强的耐受能力，可以认为都是比较成功的。关于空间电荷效应耦合束流纵横向运动这一判断，可以通过模拟计算加以说明。计算中截止能量设置得较大，可以认为粒子丢失基本发生在横向。模拟计算了第 2 套设计方案中注入流强 0 mA时束流的传输情况，这时相当于没有空间电荷效应。当注入能量同样偏离设计值 10%时，传输效率仍然在 99%左右。这就说明没有空间电荷效应时纵横向运动间无耦合。1

微波振荡器的束流动力学与束－波转换效率研究背景将微波技术向太赫兹波段推进时，人们常常关注的是器件频率、效率和功率等问题。描述电磁运动规律的Maxwell方程，场分布仅与边界条件有关。换句话说，不同的腔体有不同的场分布，与束流是否存在无关。束流强度只影响场强和相位。束－波转换效率和辐射功率则主要取决于电子束的群聚和束－波相互作用。束－波相互作用过程是一个自洽过程。一方面，微波场的存在影响电子运动；另一方面，在微波场中运动的电子，因加速度不为零将产生电磁辐射影响微波场。对微波器件的不同要求（比如频率、效率和功率）决定了腔体的不同选择。我们感兴趣的腔体是一个带有漂移空间的两腔结构，腔体中的微波场是周期场，并假设第一个腔体比第二个腔体长得多。试图从经典物理学出发，对这种结构的束流动力学进行分析。在经典力学框架内，把电子相位运动方程化为摆方程；并从系统的相平面特征出发，讨论了器件的接受度和束－波转换效率。

研究进展一般说来，强流粒子束的空间电荷效应很重要，但是在一些情况下它的影响可以不考虑。比如我们关心的问题就可以忽略它的影响。注意到空间电荷包含直流和交流两种成分，由于强引导场，直流部分很弱可以不考虑；而交流成分则主要影响电子束群聚，在俘获阶段也可以忽略，因为在这个阶段电子束分布比较均匀，交流成分很弱；又因漂移空间的长度远大于电子束的等离子体波长，交流影响也可以不考虑。因此略去空间电荷的影响。

注意到任何假设都是近似的，假设了引导场足够强，三维问题可以化为一维问题；假设了电场只有轴向分量，且场分布是周期的；假设了第一个腔足够长，第二个腔足够短；还假设了空间电荷效应可以忽略。在这些近似下，对两腔微波振荡器的束流动力学与束－波转换效率进行了讨论。当相空间密度均匀分布时，相面积越大束流越强，功率越高；而能散越大束－波作用越强，转换效率越高。这正是微波器件期待的。2

弯晶与同步加速器的束流动力学稳定性20 世纪 60 年代，人们在研究带电粒子同晶体相互作用的过程中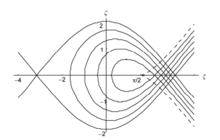发现了沟道效应；1976 年，前苏联科学家 Tsyganov预言了可以利用弯晶来控制带电粒子运动方向。1979 年，DUBNA 联合核子研究所的科学家们在实验上首次发现了弯晶沟道现象，并同欧洲核子研究中心(CERN)和列宁格勒的科学家们一道对这一现象进行了研究。1984 年，DUBNA 首次实现了对能量为 1 GeV 的质子束偏转。1989 年，前苏联高能物理研究所IHEP把这一技术纳入了它的中长期科学发展规划，并在1996 年，实现了对能量为 70GeV 质子束的控制，引出效率达到了85%，而束流强度也达到 4×1012 粒子；同年，欧洲 CERN 也实现了对能量为120 GeV 和450 GeV 质子束的偏转；而美国费米国家实验室(Fermilab)则实现了更高能量(900 GeV)的质子束控制。欧洲大型粒子加速器LHC也试图采用这一引出技术。

近年来，弯晶的束流控制技术得到了迅速发展。事实证明，利用弯晶控制正的带电粒子是非常有效的，只需在束流通道上放上一定长度的常曲率弯晶或变曲率弯晶，即可实现对束流的准直、切割、偏转和引出等。注意到在加速器技术中，粒子能量和束流强度是人们始终追求的目标，而本文关心的引出技术和引出效率则是提高束流强度的关键。弯晶的束流控制很大程度上决定于粒子的退道长度，退道长度越长元件的性能越好，引出效率越高。值得注意的是弯晶的退道长度与系统的稳定性有关。试图对这个问题进行分析。首先，在经典力学框架内和偶极近似下，把粒子在弯晶中的运动方程化为具有固定力矩、具有阻尼项和受迫项的广义摆方程。3

本词条内容贡献者为:

李勇 - 副教授 - 西南大学