[科普中国]-部分子分布函数

上个世纪六十年代末，在SLAC上进行的带电轻子-核子深度非弹性实验让人们第一次认识到核子是由许多类点物质组成，这些物质就被称为部分子。为了描述核子在动力学过程中内部部分子的变化情况，引入了部分子分布函数。

函数关系部分子分布函数 部分子在水平上研究高能作用的最基本的物理量。利用部分子分布函数可以计算出双喷柱关联，单举散射截面及带电粒子多重分布，其函数关系式如下：

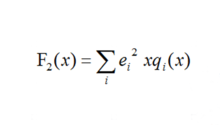
其中i是指核子中夸克种类数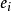，是第i种夸克所带的电量，x是夸克所带有的动量占核子动量的比例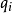，(x)是第i种夸克的分布函数。部分子分布函数可分为积分的与未积分的部分分布函数，这里的分布函数是积分的分布函数。

分类积分部分子分布函数积分部分子分布函数可用来描述深度非弹性散射实验中的单举反应、核子的内部结构等，它满足传统的扭度-2DGLAP方程。但是当部分子的密度很大时就必须考虑它们之间的相互作用，出现遮蔽效应，即高扭度现象。扭度-4DGLAP方程2修正后的演化方程。通过这两个演化方程得到的积分部分子分布函数有着一定的差异性。当考虑Drell-Yan等高能过程时，横动量过得作用则变得很重要，部分子不再依赖于一个标度，而要引入未积分部分子分布函数。

未积分部分子分布函数未积分部分子分布函数没有对横动量进行积分的函数，它可由CCFM方程得到，但是CCFM方程只用于蒙特卡罗方法计算，非常复杂。

研究现状夸克的色禁闭性使得人们没有办法直接测出部分子的分布函数，必须通过拟合截面等试验数据来确定积分部分子初始函数分布，然后根据演化方程得到大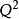下的积分分布函数，但是非微扰的标度没有定论，不同的实验小组如GRV、MARST等均提出了在不同的固定演化起点下的初始演化分布。标准动力学演化方程考虑了扭度-2效应，这时就需考虑扭度-4效应了。

虽然对核子中的未积分部分子分布函数进行了理论和实验方面的研究，但是对未积分部分子分布函数了解还是不够多，究其原因主要在于：未积分部分子分布函数至少依赖两个变量（x和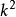）,微扰区域与非微扰区域的界限并没有定论。一般采用的是GBW(Golec-Biernat-Wusthoff)模型，BFKL模型和KMR模型等。不同模型和初始分布下的未积分部分子分布函数都能解释某些实验现象，但是它们之间的共同性还不是很清楚。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学