[科普中国]-失量场

矢量场是由一个向量对应另一个向量的函数。矢量场广泛应用于物理学，尤其是电磁场。

概述在矢量运算，一个矢量场是一个分配矢量的每个点中的一个子集的空间。平面中的矢量场（例如）可以被形象化为：具有给定幅度和方向的箭头集合，每个箭头都连接到平面上的一个点。矢量场通常被用来模拟例如流体在整个空间中的速度和方向，或者某个力的强度和方向，比如磁力或者引力，随着它从一个点到另一个点的变化。

微分和积分的元素自然延伸到矢量场。当矢量场表示力时，矢量场的线积分代表沿着路径运动的力所做的功，在此解释下，能量守恒作为微积分基本定理的一个特例展现出来。矢量场可以被有效地理解为表示流动的流动在空间中的速度，并且这种物理直觉导致了诸如散度（其表示流量的变化率）和卷曲（其表示旋转一个流程）。

在坐标中，n维欧几里得空间上的一个域上的矢量场可以表示为一个矢量值函数，它将实数的n个元素与该域的每个点相关联。矢量场的这种表示取决于坐标系，并且从一个坐标系到另一个坐标系存在明确的变换规律。矢量场通常在欧几里德空间的开放子集上进行讨论，但是在其他子集（例如曲面）上也是有意义的，在这些子集上，每个点（切线矢量）将曲面的切线与曲面相切。

更一般地说，矢量场定义在可微的流形上，这些流形看起来像欧氏空间的小尺度空间，但在更大尺度上可能会有更复杂的结构。在该设置中，矢量字段给出在歧管的各点处的切线向量（即，部分所述的切丛到歧管）。矢量场是一种张量场。1

定义设X是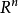 里的一个连通开集，一个矢量场就是一个向量函数：

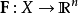
我们称F为一个C矢量场，如果F在X上是k次连续可微的。

在X内，一个点x被称为固定的，若

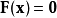
矢量场可以理解为一个n维空间，其中对X内每一个点都有个附着的n维向量。

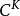
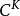给定两个定义于X上的 矢量场F，G以及一个定义于X上的实值函数f，可以定义以下运算：

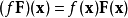
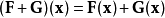
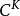
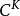如此便可定义在函数的环上的矢量场的模。1

矢量场的操作线积分物理学中常见的技术是沿着曲线积分矢量场，即确定其线积分。给定一个引力矢量场中的粒子，其中每个矢量表示在空间中给定点处作用于粒子上的力，线积分是粒子在沿着特定路径传播时所做的功。

线积分类似于黎曼积分构造，如果曲线是可纠正的（有限长度）并且矢量场是连续的，则线积分存在。

给定矢量场V和由[a，b]（其中a和b是实数）参数化的曲线γ，线积分定义为1：

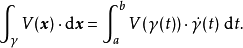
发散欧几里得空间上的矢量场的发散是一个函数（或标量场）。在三维中，分歧由下式定义：

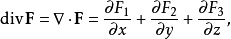
明显可泛化为任意维度。一点处的发散表示点周围的小体积是向量流的源或汇的程度，其结果由发散定理精确地确定。

散度也可以在黎曼流形上定义，也就是用黎曼度量的矢量长度的流形。1

三维卷曲卷曲是取矢量场，并产生另一矢量场的操作。卷曲仅在三维中定义，但是卷曲的一些属性可以通过外部导数在较高维度中捕捉。在三维中，它被定义为：

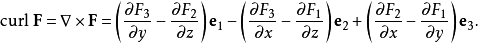
卷曲测量矢量流在一个点处的角动量的密度，即流量绕固定轴循环的量。这个直观的描述是由斯托克斯定理精确。1

矢量字段的索引矢量场的索引是一个整数，有助于描述孤立零点（即场的孤立奇点）周围的矢量场的行为。在平面上，索引在鞍点奇异值处取-1，而在源或奇点处取+1。

设矢量场定义的流形维数为n。在零点周围取一个小的球体S，使得S的内部不会有其他的零点。从这个球体到一个尺寸为n-1的单位球体的映射可以通过将这个球体上的每个向量除以它的长度来构成单位长度矢量，它是单位球面S上的一个点。这定义了从S到S的连续映射。该点处的矢量场的索引是该地图的度数。可以证明这个整数不依赖于S的选择，因此只依赖于矢量场本身。

当矢量场的索引只有有限个零时，就定义了整个矢量场的索引。在这种情况下，所有的零都是孤立的，矢量场的索引被定义为所有索引的和。

该索引没有在任何非奇异点（即，向量不为零的点）上定义。对于三维空间中的普通（二维）球体，可以表明球体上的任何矢量场的索引必须具有零，即选择向量以一种连续的方式，使得它们都是非零的，并与S相切。

对于有限个零点的紧致流形上的矢量场，Poincaré-Hopf定理指出矢量场的指数等于流形的欧拉特征。2

坐标转换法在物理学中，矢量的另一个区别在于，当一个矢量相对于不同的背景坐标系统测量相同的矢量时，它的坐标是如何变化的。向量的转换属性将向量区分为几何不同的实体和简单的标量列表，或者来自covector。

因此，假设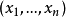 是直角坐标系的选择，无论在哪个的向量的分量V是：

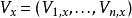
并且假设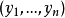 是定义不同坐标系的xi的n个函数。然后在新的坐标中矢量V的分量需要满足变换规律：

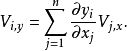
这种转化法则被称为逆变。一个类似的变换法则表征了物理中的矢量场：具体地说，矢量场是每个坐标系中n个函数的规范，服从关于不同坐标系的变换定律。

矢量场因此与标量场相对比，标量场将数字或标量与空间中的每个点相关联，并且与标量场的简单列表形成对比，标量场在坐标变换下不变换。2

物理应用1、铁棒的磁力线（磁偶极子）；

2、迈克尔·法拉第，在他的概念的力线，谁强调，场本身应该是研究的对象，它已经成为整个物理学场论的形式。除了磁场之外，法拉第建模的其他现象还包括电场和光场。1

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学