干扰观测器是将外部干扰以及模型参数变化造成的实际对象与名义模型之间的差异等效到控制输入端,即观测出等效干扰。并在控制中引入等效的补偿,实现对干扰的完全控制。
基本原理干扰观测器的基本结构如图。图中的Gp(S)为对象的传递函数,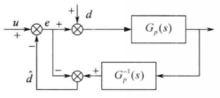 d为等效干扰,
d为等效干扰, 为观测干扰,u为控制输入。由图可以求出等效干扰的估计值
为观测干扰,u为控制输入。由图可以求出等效干扰的估计值 为
为
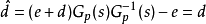
对于实际的物理系统,其实现存在如下问题:
(1)通常情况下,Gp(s)的相对阶不为零,其逆在物理上难以实现。
(2)对象Gp(s)的精确数学模型无法得到。
(3)考虑到测量噪声的影响,该方法的控制性能将下降。
解决上述这些问题的唯一方法是在 的后面串人低通滤波器Q(s),
的后面串人低通滤波器Q(s), 并用名义模型
并用名义模型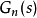 的逆
的逆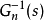 来代替
来代替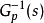 ,从而得到如图所示的干扰观测器框图,其中虚线框部分为干扰观测器。
,从而得到如图所示的干扰观测器框图,其中虚线框部分为干扰观测器。
控制器的输出为
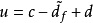
式中:c为改进的变饱和状态柔性变结构控制器的输出;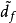 为干扰d的估计值;n为传感器的等效测量误差。由上式可知,当干扰观测器预测得到的干扰也等于系统干扰d时,改进的变饱和状态柔性变结构控制器的输出即为系统的控制输入,干扰对系统的影响被降低到最小。由图可知,
为干扰d的估计值;n为传感器的等效测量误差。由上式可知,当干扰观测器预测得到的干扰也等于系统干扰d时,改进的变饱和状态柔性变结构控制器的输出即为系统的控制输入,干扰对系统的影响被降低到最小。由图可知,
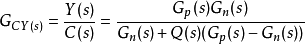
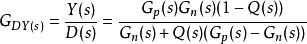

设低通滤波器Q(s)的频带为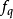 ,则:
,则:
当 时,
时,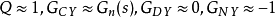 ;
;
当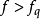 时,
时,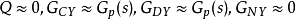 。
。
通过低通滤波器Q(s)的设计可较好地抵抗外加干扰。由上面的分析可见,
Q(s)的设计是干扰观测器设计中的一个重要环节。首先,为使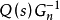 正则,Q(s)的相对阶应不小于
正则,Q(s)的相对阶应不小于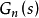 的相对阶;其次,Q(s)带宽的设计应是在干扰观测器的鲁棒稳定性和干扰抑制能力之间的折中。
的相对阶;其次,Q(s)带宽的设计应是在干扰观测器的鲁棒稳定性和干扰抑制能力之间的折中。
设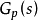 的名义模型为
的名义模型为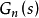 ,则不确定对象的集合可以用乘积摄动来描述,即
,则不确定对象的集合可以用乘积摄动来描述,即
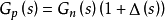
式中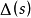 为可变的传递函数。在仿真时,可设
为可变的传递函数。在仿真时,可设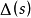 是一个固定的等效误差值,也可设置为一个变化的随机值,它表示实际对象模型对于名义模型的摄动。
是一个固定的等效误差值,也可设置为一个变化的随机值,它表示实际对象模型对于名义模型的摄动。
由鲁棒稳定性定理,干扰观测器鲁棒稳定的充分条件是
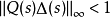
上式是Q(s)设计的基础,通过Q(s)的设计,可实现鲁棒性要求。忽略非建模动态不确定性的影响,对一个二阶系统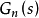 常可描述为
常可描述为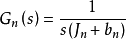 。式中,
。式中, 为等效惯性力矩;
为等效惯性力矩;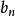 为等效阻尼系数。
为等效阻尼系数。
采用的Q(s)结构的标准形式为

选择不同的 值,Q(s)滤波器对应不同的截止频率
值,Q(s)滤波器对应不同的截止频率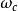 。增加
。增加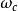 的值可以增加Q(s)的带宽,而且能够更加有效地抑制干扰。但是随着
的值可以增加Q(s)的带宽,而且能够更加有效地抑制干扰。但是随着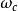 的增加,系统的稳定性会降低,甚至导致系统不稳定。因此,
的增加,系统的稳定性会降低,甚至导致系统不稳定。因此,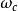 的选择要兼顾到系统的稳定性和抗干扰效果。理论上Q(s)的阶数越高,系统的动态性能就越好,但会出现不稳定的问题。1
的选择要兼顾到系统的稳定性和抗干扰效果。理论上Q(s)的阶数越高,系统的动态性能就越好,但会出现不稳定的问题。1
改进的干扰观测器设计干扰观测器在对干扰进行估计时,不需要对于扰信号建立准确的数学模型,而且它本身的结构也比较简单,因此在预测干扰信号时避免了大量的数学计算,这有利于满足实时性的要求。在系统设计时,考虑到系统的干扰可以归结为外部扰动以及由于执行机构和其理想数学模型之间的参数变化而产生的误差。因此,如果能够利用干扰观测器对干扰信号进行有效的预测并加以补偿,那么在一定的误差范围内就可以将实际执行机构的模型用其参考模型来等价。
参考干扰观测器的基本原理图,并根据所要控制系统的特点,对图二中的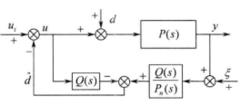 干扰观测器作了改进,其结构如图三所示。 图三中,
干扰观测器作了改进,其结构如图三所示。 图三中,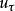 为参考输入,u为控制器输出,d为系统的外部干扰,
为参考输入,u为控制器输出,d为系统的外部干扰, 为传感器的等效测量误差,
为传感器的等效测量误差,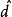 为干扰观测器的输出即预测到的系统干扰。
为干扰观测器的输出即预测到的系统干扰。
由图6.5可得系统的输出y的表达式如下:
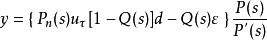
式中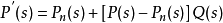 ,假定P(s)代表实际执行机构,
,假定P(s)代表实际执行机构,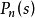 为其参考模型,Q(s)为干扰观测器的低通滤波器。当低于Q(s)的截止频率即处于低频段时,如果取
为其参考模型,Q(s)为干扰观测器的低通滤波器。当低于Q(s)的截止频率即处于低频段时,如果取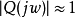 ,那么P(s)的输人输出特性就等价于其理想参考模型尸。
,那么P(s)的输人输出特性就等价于其理想参考模型尸。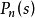 的输人输出特性;当高于Q(s)的截止频率时,如果取
的输人输出特性;当高于Q(s)的截止频率时,如果取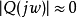 ,那么就会减小传感器的高频测量误差对系统的影响。因此,干扰观测器设计的关键是其低通滤波器参数的选择。
,那么就会减小传感器的高频测量误差对系统的影响。因此,干扰观测器设计的关键是其低通滤波器参数的选择。
低通滤波器的性能决定整个干扰观测器的动态特性。从理论上分析,如果Q(s)的带宽越宽,阶数越高,那么干扰观测器的响应速度就越快,对干扰的抑制效果就越好,干扰对系统的影响越小即系统对干扰的灵敏度越低。但是随着阶数的升高,由于大的相位滞后使系统产生欠阻尼现象,甚至使系统变得不稳定。因此,如何使干扰观测器获得好的动态特性和高的稳定性是Q(s)设计的关键。
本词条内容贡献者为:
宋春霖 - 副教授 - 江南大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国