[科普中国]-鲁棒阻尼控制

鲁棒阻尼控制是指激励力的频率在受迫振动系统的共振频率附近的一个频段内，系统所表现出的振动性质。这时，振动系统的阻抗主要决定于系统的阻尼。振动的速度近似与频率无关，而与阻尼常数成正比。根据这一性质，可以用增大阻尼的方法，抑制系统（例如传声器、隔振器）在共振频率附近的响应峰值。

简介鲁棒性所谓鲁棒性，是指控制系统在一定（结构，大小）的参数摄动下，维持某些性能的特性。根据对性能的不同定义，可分为稳定鲁棒性和性能鲁棒性。以闭环系统的鲁棒性作为目标设计得到的固定控制器称为鲁棒控制器。
性能指标的鲁棒性分析方法也可分为频域和时域两种，使用何种性能指标，要视提出的性能指标是在频域还是在时域而定。1

鲁棒控制鲁棒控制（RobustControl）方面的研究始于20世纪50年代。在过去的20年中，鲁棒控制一直是国际自控界的研究热点。鲁棒控制的早期研究，主要针对单变量系统（SISO）的在微小摄动下的不确定性，具有代表性的是Zames提出的微分灵敏度分析。然而，实际工业过程中故障导致系统中参数的变化，这种变化是有界摄动而不是无穷小摄动，因此产生了以讨论参数在有界摄动下系统性能保持和控制为内容的现代鲁棒控制。
实验中总是假设已经知道了受控对象的模型，但由于实际中存在种种不确定因素，如：

参数变化；
未建模动态特性；
平衡点的变化；
传感器噪声；
不可预测的干扰输入

所以所建立的对象模型只能是实际物理系统的不精确的表示。鲁棒系统设计的目的就是要在模型不精确和存在其他变化因素的条件下，使系统仍能保持预期的性能。如果模型的变化和模型的不精确不影响系统的稳定性和其它动态性能，这样的系统就称它为鲁棒控制系统(robust control system)。1

鲁棒控制理论是分析和处理具有不确定性系统的控制理论，包括两大类问题：鲁棒性分析及鲁棒性综合问题。主要的鲁棒控制理论有：

Kharitonov区间理论；
H∞控制理论；
结构奇异值理论（μ理论）；

鲁棒调节器设计Davison提供的鲁棒调节器由两部分组成，一是伺服补偿器，二是镇定补偿器。伺服补偿器是按设定与扰动作用的变化形式(如阶跃变化、斜坡函数变化等)来确定的，以达到无稳态偏差的要求。镇定补偿器的作用是使系统在参数变化条件下仍保持稳定，并有一定裕度。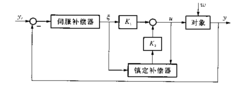

鲁棒调节器的一般形式为：
μ= K1 ξ +K2η
式中K1，K2 为增益矩阵,ξ为伺服补偿器输出,η为镇定补偿器输出

主要研究鲁棒控制的早期研究，主要针对单变量系统（SISO）的在微小摄动下的不确定性，具有代表性的是Zames提出的微分灵敏度分析。然而，实际工业过程中故障导致系统中参数的变化，这种变化是有界摄动而不是无穷小摄动。因此产生了以讨论参数在有界摄动下系统性能保持和控制为内容的现代鲁棒控制。

现代鲁棒控制是一个着重控制算法可靠性研究的控制器设计方法。其设计目标是找到在实际环境中为保证安全要求控制系统最小必须满足的要求。一旦设计好这个控制器，它的参数不能改变而且控制性能能够保证。

鲁棒控制方法，是对时间域或频率域来说，一般要假设过程动态特性的信息和它的变化范围。一些算法不需要精确的过程模型，但需要一些离线辨识。

一般鲁棒控制系统的设计是以一些最差的情况为基础，因此一般系统并不工作在最优状态。常用的设计方法有：INA方法，同时镇定，完整性控制器设计，鲁棒控制，鲁棒PID控制以及鲁棒极点配置，鲁棒观测器等。

鲁棒控制方法适用于稳定性和可靠性作为首要目标的应用，同时过程的动态特性已知且不确定因素的变化范围可以预估。飞机和空间飞行器的控制是这类系统的例子。

过程控制应用中，某些控制系统也可以用鲁棒控制方法设计，特别是对那些比较关键且（1）不确定因素变化范围大；（2）稳定裕度小的对象。

但是，鲁棒控制系统的设计要由高级专家完成。一旦设计成功，就不需太多的人工干预。另一方面，如果要升级或作重大调整，系统就要重新设计。

最新应用柔性直流附加鲁棒阻尼控制器设计针对包含柔性直流（VSC-HVDC）的交直流互联系统区间低频振荡现象,提出把基于线性矩阵不等式的多目标控制方法应用到柔性直流附加控制中。具体包括运用最小二乘-旋转不变方法（TLS-ESPRIT）辨识出系统降阶模型,综合考虑控制器的鲁棒性和控制代价,设定多目标函数,设计出H2/H∞多目标鲁棒附加阻尼控制器,并设计传统极点配置控制器进行比较。在PSCAD/EMTDC中搭建包含柔性直流的四机两域电磁暂态模型,特征值分析和时域仿真结果表明：在系统内部参数发生较大变化情况下,多目标鲁棒阻尼控制器具有更好的阻尼特性,并兼顾了控制器的控制代价。

静态H∞回路成形法的多通道鲁棒阻尼控制通过附加鲁棒阻尼控制器来同时抑制次同步振荡和低频振荡，通过求解线性矩阵不等式直接求解出控制器，采用总体最小二乘旋转不变技术辨识出系统振荡模态及降阶模型，利用巴特沃兹带通滤波器将系统不同振荡模态分解为多个通道，根据静态H ∞ 回路成形法针对不同的通道设计鲁棒阻尼控制器，降低控制器间相互影响。与传统的比例‑积分‑微分（PID）控制器相比结果表明，具有更好的控制效果，能同时抑制次同步振荡和低频振荡，具有较好的鲁棒性；同时所设计的控制器阶数较低，采用输出反馈，便于工程实践，且具有计算量较小，算法复杂度较低等特点。2

本词条内容贡献者为:

李岳阳 - 副教授 - 江南大学