[科普中国]-凸合作博弈

现代博弈论通常分为两部分：竞争博弈与合作博弈．纳什(Nash)和他提出的纳什均衡是竞争博弈的基础，沙普利(Shapley)等人是合作博弈的代表人物。凸合作博弈是一种特殊的合作博弈。

定义一个合作博弈(N，v)称为凸合作博弈，如果它满足

1

定理凸合作博弈的核心非空.

证明 记N=[1,2,…，n]，令

下面证明 显然x(N)=v(N).设 ，记

令 则有

利用凸性，可得

结合定得

也就是

所以

用 代替R， 代替 ，上式可变为

重复t次即得

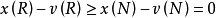
定理得证1.

应用弥补模糊合作博弈系统的传统核心解常常为空，且在很大程度上具有限制性的缺陷．采用加入相关因子方法对模糊合作博弈的核心及稳定集进行了一定的延拓，而且把凸性引入了模糊合作博弈系统中，进而给出了凸模糊合作博弈系统延拓的核心及稳定集的基本概念和特征，证明它们之间的联系能很好的解决分配方案的限制性2．

近年来，解集的本质连通区发展成为研究非线性问题稳定性的一个重要方面。其在研究优化问题的解、Nash平衡、不动点的稳定性中，发挥着关键性的作用。对于每一n人非合作博弈，至少存在一个Nash平衡点集的连续强本质连通区。在此基础之上，可讨论若干策略稳定集概念的强弱关系。空间的凸性是不动点理论以及连续选择理论中的关键条件。对抽象凸结构的性质做进一步的研究。给出抽象凸空间中上半连续集值映射的一个新的不动点定理；将Ky Fan引理、Ky Fan变分不等式定理、极大极小定理以及Schauder不动点定理推广至抽象凸空间。作为应用，证明抽象凸空间Nash平衡点的存在性。记M为所有抽象凸空间中KKM映射T组成的集合、F(T)为T的所有KKM点组成的集合。证明存在一M的稠密剩余子集Q，使得对于每一T∈Q；T为稳定的；以及对于每一T∈M，至少存在一F(T)的本质连通区。同时，应用抽象凸空间中的KKM方法可给出抽象凸空间中的“抉择定理”与“重合定理”3。

本词条内容贡献者为:

宋春霖 - 副教授 - 江南大学