[科普中国]-网络演化博弈

相关简介博弈论

博弈研究的对象是游戏(Game)，更确切的说，是指在具有双方相互竞争对立的环境条件下，参与者依靠所掌握的信息，在一定的规则约束下，各自选择策略并取得相应结果(或收益)的过程。博弈论就是使用数学模型研究冲突对抗条件下最优决策问题的理论。
博弈论被认为是研究自然和人类社会中普遍存在的合作行为最为有力的手段。博弈模型反映了自私的个体之间的合作竞争关系，能够很好地刻画生物系统中生物体之间的相互作用关系及演化动力学。
通常博弈由以下4个部分所组成:

(1)博弈个体：在一个博弈中至少有两位决策者(agent)参与博弈.

(2)策略集：个体的博弈策略可以是纯策略，也可以是混合策略博弈的策略集由参与博弈的个体所有可能采用的策略所组成.
(3)收益矩阵：当博弈个体选定好自己的策略后，其所获取的收益由收益矩阵中的相应元素来确定.
(4)策略演化: 在多轮博弈过程中，博弈个体遵循自身收益最大化的最终目标，即以此目标为指导原则来进行策略调整。

经典博弈模型囚徒困境博弈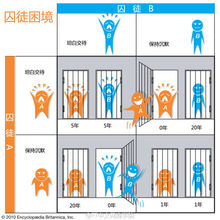

雪堆博弈

演化网络博弈基本定义要讨论合作的涌现，必须涉及相当数量的个体（局中人），而且合理地认为这些局中人以及他们之间的关系构成一个复杂网络，随着时间的演化，每个局中人都在和他的邻居进行博弈，这就称为演化网络博弈，它的定义可以表述为：
（1）数量N→∞的局中人位于一个复杂网络上。
（2）每个时间演化步，按一定法则选取的一部分局中人以一定频率匹配进行博弈。
（3）局中人采取的对策可以按一定法则更新，所有局中人的策略更新法则相同。这种法则称为“策略的策略”。然而，法则更新比博弈频率慢得多，使得局中人可以根据上一次更新对策成功与否选择、调整下一次的更新。（4）局中人可以感知环境、吸取信息，然后根据自己的经验和信念，在策略更新法则下更新策略。
（5）策略更新法则可能受到局中人所在网络拓扑结构的影响。1

演化网络博弈研究内容第一，研究网络拓扑结构对博弈演化动力学的影响。
第二，探索一些可能的支持合作行为涌现的动力学机制。
第三，研究博弈动力学和网络拓扑结构的共演化，即个体策略和网络拓扑结构协同演化的情形。2

促进合作行为涌现的机制重复博弈（争锋相对、冷酷策略）、巴普洛夫策略、亲缘选择、直接互惠、间接互惠（声誉）、网络互惠以及群选择。
公共利益博弈

演化博弈论与经典博弈论的区别（1）策略内涵的不同：不同行为 到生物系统中的不同类型物种本身，策略由物种的不同表现型来体现；
（2）均衡意义的不同：纳什均衡到演化稳定策略(ESS)；

（3）个体互相作用方式的不同（博弈个体与博弈次数）

网络上的演化博弈研究方向(1)研究网络拓扑结构对博弈动力学演化结果的影响;
(2) 一定的网络结构下，探讨各种演化规则对演化结果的影响;
(3)网络拓扑和博弈动力学的共演化，主要是自 适应网络上博弈动力学 ,即网络拓扑调整受博弈动力学影响.

网络演化博弈的策略更新规则(1)模仿最优者：即在每轮博弈过后，个体采取其邻居中获得最高收益的个体的策略进行下一轮博弈。
(2)模仿优胜者：即个体在策略更新时，同时参考那些收益比自身高的邻居的策略，以正比于他们所得收益的概率进行策略转变。
以上两种规则可以统称为模仿策略. 模仿策略的基本思想是个体的更新策略，根据邻居中收益最高的个体策略进行模仿，以期获得更高的收益。

(3)配对比较：即个体随机选择某一邻居进行收益的比较，以某个概率(为此两个体收益差的函数)转变为对方的策略!

每个节点(对应博弈者假设为P1)随机的选取他的一个邻居节点(对应博弈者假设为P2)，P1以一定概率W模仿P2的策略，常用的演化规则（统计力学的费米函数）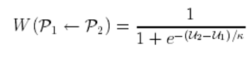

其中，Ui表示Pi的累积收益，参数κ>0为噪音，代表了一种非理性行为的可能，一般是一个很小的值，常取0.1。当κ→∞时，表示所有的信息都被噪音淹没，策略进行完全随机的更新；当κ→0时，表示确定的模仿规则，即当P2的累积收益高于P1时，P1则采取P2的策略。
另一类演化规则

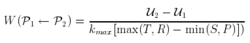
其中，kmax为P1与P2中较大度节点的度，P,T,S,R为2×2收益矩阵元素。

(4)随机过程方法：通常考虑Moran过程(birth一death) (或者death一birth过程) ， 即在策略更新时，以正比于个体适应度(由收益来衡量)的概率产生一个新的个体，然后随机取代此个体的某个邻居。
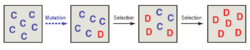
Moran过程是将Darwin的进化思想直接引入到演化博弈中。一个实际背景是种群中的变异入侵，以下图为例，种群中所有个体“C”，当某个个体发生变异后，变为”D”，以后每一步考虑随机移去一个个体，并以正比于原种群中“C”个体适应度的概率生成一个新的“C”个体，否则生成一个新的“D”个体。在适应度函数满足一定条件时，“D”个体可能完全侵占整个种群(Invade)，
Martin A.Nowak等人研究了这类种群侵占问题，将某种策略从种群中仅存在一个变异个体时，最终能侵占整个种群的概率定义为策略的扎根概率。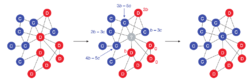

死生过程是Moran过程的一个自然推广，原始网络中存在合作“C”、背叛“D”两种策略，按照连边关系个体之间进行博弈，获得一个累计收益，其中b表示合作收益，即遇到对手采取合作时获得收益；c表示合作代价，即个体采取合作获得负收益。随机选择选择一个个体死亡(假设为位于中间位置的“D”节点)，则其所有的邻居按照正比于个体适应度的概率产生一个后代，填补个体死亡后留下的空位。重复这一过程，种群中的策略将达到动态平衡。