[科普中国]-联合子区间法

联合子区间法预测苹果糖度

由于糖度是一个反映多种物质综合作用的指标，因此用一个单独的狭小子区间(即使有所扩张)来预测苹果的糖度是不可行的。但同时，这一结果也提示了以较少波数点来获得较高预测精度的另一种区间选取方法，即将同一次区间划分中精度较高的几个局部模型所在的区间联合起来共同预测苹果糖度(称其为联合子区间法)。图1分别列出了将光谱划分为10，11，…，20个子区间后，各最优联合模型的建模区间，从表中可以看出，参加建立联合最优模型的波数点数目都减少了一半以上，其中，波数点数目减少最多的联合最优模型产生于将整个光谱区域划分为19个子区间时，该模型建立于第1、5、6、7、8、11、12号子区间之上，只利用了553个波数点。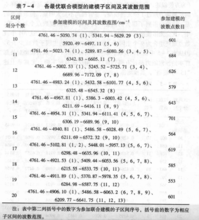

图2所示为各最优联合模型的性能，从表中可以看出，采用多个子区间联合建模后，糖度偏最小二乘模型的校正性能都较建立于单一子区间上的模型有所改善，它们的交互验证均方根误差RMSECV值都降到了0.55以下，比最优局部模型(基于区间“14—4”的模型)的RMSECV值下降了26%以上，相关系数r2也有了明显的提高。特别是将光谱划分为15个子区间时，利用其中的第1、4、5、6、7、9、10号等7个子区间联合建立的糖度模型(为方便叙述，将其简称为“15—7”模型)，其对交互验证集样本的预测能力超过了全光谱模型，尽管提高不是太明显，但最重要的是，该模型得到了很大的简化：其实际采用的波数点个数为701个，比全光谱模型采用的波数点个数减少了一半以上；这701个波数点最终组合为9个主因子，比全光谱模型的主因子数减少了3。但从图2中也可以发现，研究中所得到的11个联合模型对外部样本的预测能力都没有得到提高，相反还有所下降，尤其是上述“15—7模型”，其预测能力的下降最为明显。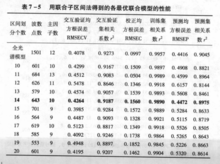

从简洁性、预测能力等方面来综合评价，将全光谱划分为14个子区间时，建立于第1、4、5、6、8、9号等6个子区间之上的模型是11个最优联合模型中最佳的(见图2中粗体行所示)，该模型只利用了643个波数点，采纳的主因子数为10，与全光谱模型相比，该模型的预测能力有所下降。

从上面的结果可以看出，将精度较高的几个局部模型所在的子区间联合起来建立一个糖度预测模型是可行的。但目前尚不能从理论上确定参加联合建模的子区间数目1。

区间偏最小二乘法的算法常规区间偏最小二乘法常规区间偏最小二乘波长筛选法(iPLS)是由Lars Norgaard于2000年提出的一种波长筛选法，该法主要用于筛选偏最小二乘建模的波长区域，其算法步骤如下：

(1)对原始光谱进行预处理；

(2)在全光谱范围内建立待测品质的偏最小二乘模型(这里称为全局偏最小二乘模型)；

(3)将整个光谱区域划分为多个等宽的子区间，假设为n个；

(4)在每个子区间上进行偏最小二乘回归，建立待测品质的“局部回归模型”，也就是可以得到n个局部回归模型；

(5)以交互验证时的均方根误差RMSEC值为各模型的精度衡量标准，分别比较全光谱模型和各局部模型的精度，取精度最高的局部模型所在的子区间为人选区间；

(6)对入选的区间进行优化，即以(5)中选定的区间为中心，单向或双向扩充波长区域，最终得到一个最佳的波长区间。

由于农产品是组成非常复杂的天然生物体，其内部指标并不是以某种纯的化学成分存在，单独的一个小区间是不能提供足够的信息来预测农产品指标。联合区间偏最小二乘法和后面的向前/向后区间偏最小二乘法就是在这种情况下提出来的。从理论上讲，联合几个子区间建立的预测模型，精度将更高2。

联合区间偏最小二乘法联合区间偏最小二乘法是建立在常规区间偏最小二乘法的基础上的一种方法，它将同一次区间划分中精度较高的几个局部模型所在的子区间联合起来，共同预测农产品品质指标(称其为联合子区间法)。实际应用表明，将精度较高的几个局部模型所在的子区间联合起来建立的预测模型是可行的。但目前尚不能从理论上确定参加联合建模的子区间数目。

向前区间偏最小二乘筛选法的基本原理向前阈值区间偏最小二乘筛选法(FiPLST)基于Lars NФrgaard的iPLS理论，同时引进了向前选择变量法的思想，是一种“只进不出”的方法，其算法步骤如下：

(1)对原始光谱进行预处理；

(2)在全光谱范围内建立待测品质的偏最小二乘模型(这里称为全局偏最小二乘模型)；

(3)将整个光谱区域划分为多个等宽的子区间，假设为n个；

(4)在每个子区间上进行偏最小二乘回归，建立待测品质的“局部回归模型”，也就是可以得到n个局部回归模型；

(5)以交互验证时的均方根误差RMSECV值为各模型的精度衡量标准，分别比较全光谱模型和各局部模型的精度，取精度最高的局部模型所在的子区间为第一入选区间；

(6)将余下的(n一1)个子区间逐一与第一入选子区间联合，产生(n一1)组联合区间，并在每一联合区间上进行偏最小二乘回归，得到(n一1)个联合模型，选择其中RMSECV值最低的模型所在的子区间为第二入选区间。这样运行下去，直至余下所有子区间都将进入联合模型；

(7)考察第(6)步中每次联合模型的RMSECV值，找出在所有模型中选出性能最佳者(RMSECV最小)，其所对应的区间组合即为最佳组合。

向后区间偏最小二乘筛选法的基本原理向后区间偏最小二乘法是一种“只出不进”的方法，其算法(1)、(2)、(3)与FiPLS法一样；

(4)每次去掉1个子区间，在余下(n一1)个联合区间进行偏最小二乘回归，得到n个联合区间的回归模型；

(5)以交互验证时的均方根误差RMSECV值为各模型的精度衡量标准，分别比较各联合模型的精度，取精度最高的联合模型时所去掉的子区间为第一去掉子区间；

(6)将余下的(n一1)个子区间逐一去除一个子区间，产生(n一1)组联合区间，并在每一联合区间上进行偏最小二乘回归，得到(n一1)个联合模型，选择其中RMSECV值最低的模型所对应去除的子区间为第二去除的区间。这样运行下去，直至剩下一个子区间模型；

(7)与FiPLS法一样。可以看出，向影向后区间偏最小二乘筛选法(FiPLS/BiPLS)采用的仍然是几个子区间联合建模的方法，但其区间的搜寻方法继承了向前/向后选择变量法“只进不出”/“只出不进”的特点，因此可以很方便地确定联合模型的建模区间数。同时向前/向后区间偏最小二乘筛选法能在不同的区间划分(即将光谱划分为不同数目的子区间)中搜索到最佳的联合区间。从现有的应用实例来看，通过各种区间偏最小二乘法选取合适的光谱区间进行建模，可以减小建模运算时间，剔除噪声过大的变量区域，使最终建立的农产品品质指标预测模型的预测能力更强，精度更高3。