[科普中国]-龙伯格观测器

龙伯格观测器的设计

龙伯格观测器是在反馈通道设置一个补偿器，以获取不可测状态的信息，系统的一般形式如图所示。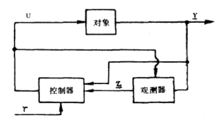

龙伯格已经证明，对于一个线性定常系统可以用状态z来建立一个(n-m)阶的观测器，使得z与由Lx给出的系统状态的一个线性组合相近似，其中L具有(n-m)维．
对于一个线性定常系统的一个(n-m)阶观测器用下式来定义：

z=Dz+Ty+Ru (1.1)

式中D，T，R分别是(n-m)×(n-m)，(n-m)×m和(n-m)×l维的常数矩阵。假设有一个满足

LA-DL=TC (1.2)
的变换L，并把矩阵月建立为：

R=LB (1.3)
于是，如果z(0)=Lx(0)，那么当所有t≥0时，z(t)=Lx(t)，或更一般地说，
z(t)=Lx(t)+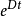 (z(0)-Lx(0)) (1.4)
这样，我们得到
z-Lx=Dz+Ty+Ru-LAx-LBu=Dz+Ty-LAx (1.5)
而根据式(1.2)代替LA，我们得到
z-Lx=D(z-Lx) (1.6)
上式具有式(1.4)作为它的一个解.
如果使观测器的特征值比被观测系统的特征值负得多，那么观测器的状态将收敛于被观测系统的状态，收敛之快足以令人满意地跟踪被观测系统的动态特性．
由方程(1.1)定义的观测器的设计取决于矩阵方程(1.2)的解，使得最后产生的矩阵工具有足够大的秩，能保证恢复那些不能测量的状态变量．如果D选择得使它的特征值都是相异的，并与A的特征值不相交，那么式(1.2)具有工的唯一解，
观测器设计的一种常用计算法是选择D，然后求出L和T．1

龙伯格观测器的应用在电液控制系统中的应用对电液控制系统进行最优控制,进行极点配置以及其它许多控制形式,都必须采取系统状态反馈的形式,但是往往得不到系统的所有状态,因此就要采用状态估值器来得到状态的估值,进而实现所要求的控制规律。鉴于电液系统的特点,采用龙伯格观测器进行降维状态估值,该装置已应用在材料试验机的电液力控制系统中,并得到满意的结果。2

在前馈控制策略中的应用针对PWM整流器采用前馈控制策略加装负载电流传感器所产生的问题,产生了一种基于龙伯格观测器理论的无电流传感器的前馈控制策略,即采用基于龙伯格状态观测器的方法取代电流传感器对负载电流进行测量,避免了安装电流传感器所带来的增加线路电感、安装位置困难等问题,尤其当母线挂接多个逆变器负载需要多个传感器时,采用该方法可大大降低成本,提高系统的可靠性。3