[科普中国]-莫特散射

概念

莫特散射（Mott scattering）是指在库仑势场的作用下，与靶核相同的入射粒子和靶核发生的弹性散射。设碰撞的原子核的原子序数为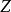，相对运动动能为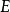，考虑了全同粒子效应，莫特散射的微分截面表达式是

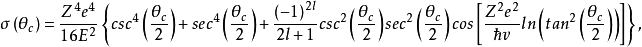其中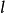是原子核的自旋，是相对运动速度。1

基本原理在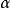粒子散射实验中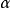，粒子的自旋为0，因此可用卢瑟福公式，但如果入射粒子为电子或质子，它们的自旋为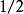，就不能用卢瑟福公式了。莫特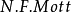（）使用了相对论的狄拉克方程讨论了自旋为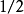、电荷为1的粒子被无自旋的靶粒子散射，这被称为莫特散射。按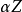的幂次展开后取到的一次幂的莫特微分散射截面为

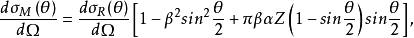这里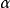是精细结构常数，。可见，莫特散射和卢瑟福散射一样，散射体的原子序数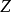越大和入射粒子能量越低，散射截面就越大，质量轻的电子的散射比质子强得多。

在能量较低时，上式中方括号内的数值接近1，莫特散射回到了卢瑟福散射。在能量较高的情况下，原子序数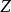小时，莫特散射的截面会超过卢瑟福散射的截面。图1给出的是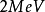的电子产生的莫特散射微分截面与卢瑟福散射微分截面之比的实验与理论比较，它们符合较好。

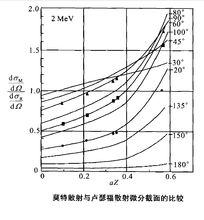
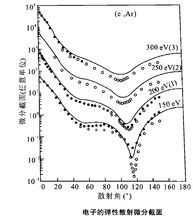
低能情况下玻恩近似不再正确，需用其他一些新发展的计算方法处理。图2给出低能电子与亚原子的弹性散射微分截面与角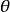的关系，它与卢瑟福散射公式给出的曲线不同，曲线形状随入射电子能量的增加有变化。图中点为实验值，曲线为理论计算值。各能量值后括号中数字表示纵坐标已乘上相应的10的幂次。

对这种电子的入射情况，应将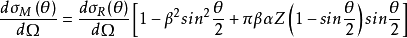式子的括号中的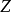用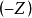代替，这时第三项永远为负值，因此正电子的莫特散射截面永远小于它的卢瑟福散射截面，并永远小于电子的莫特散射截面。2