[科普中国]-模态叠加法

概念

模态叠加法又称“振型叠加法”，它是 以系统无阻尼的振型（模态）为空间基底，通过坐标变换，使原动力方程解耦，求解n个相互独立的方程获得模态位移，进而通过叠加各阶模态的贡献求得系统的响应。

实用中，这种方法一般是保留少数振型叠加的截断形式出现，因此就产生了两种不同的方法：模态位移法和模态加速度法。

基本原理无阻尼体系下面首先通过简支梁的弯曲振动，说明用振型叠加法求解无阻尼分布参数体系动力反应的原理和做法。

分布参数梁的运动方程为：

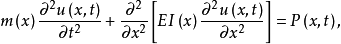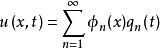将 代入上式，得：

将上式的每一项都乘上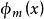 ，并积分，得：

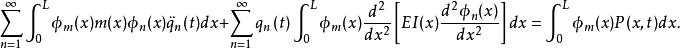
由正交条件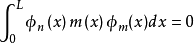 和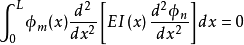 两个式子，上面的级数中除了 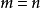项外，其余各项都等于零，于是

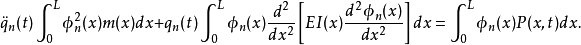
将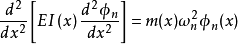 代入上式，得：

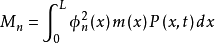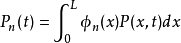记 和 分别表示第 阶振型质量和对应第 阶振型力，则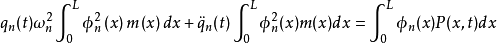 的式子可简化为

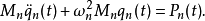
有阻尼体系对于分布参数的有阻尼体系，其运动方程为：

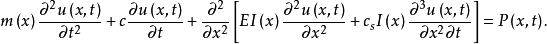
将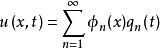 代入上式，得：

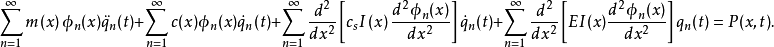
将上式的每一项都乘上 ，积分得：

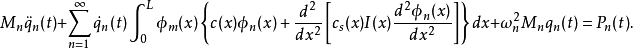
显然，在一般情况下，上式中的阻尼项相互耦联，因此需要联立方程组求解。但是，如果假定为经典阻尼，则运动房产中的阻尼项解耦，可以直接将运动方程改写为：

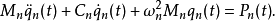
可见，体系的总反应等于各个振型贡献的叠加。与离散多自由度体系相同，对于大多数类型的荷载，分布参数体系各个振型所起的作用一般是频率最低的振型最大，高振型则趋向减小。因而在叠加过程中通常不需要包含所有的高振型，当动力反应达到精度要求时，即可舍弃级数的其余各项，从而大大减少了计算工作量。此外，对于复杂结构，其高阶振型的数学建模的可靠性相对较小，在动力反应分析时限定要考虑的振型数也是很必要的。1