[科普中国]-局部热力学平衡

概述

假如各点的物质具有一定的温度，就说物质处于局部热力学平衡。这时辐射输运理论可大大地简化，我们将区分两种情况:一种是热力学平衡存在于物质的粒子之间，另一种情况是在各点的辐射与物质达到平衡。第一种情况称之为部分的局部热力学平衡，第二种情况称之为完全的局部热力学平衡，统称为局部热力学平衡。

假如物质处于局部热力学平衡，则发射和吸收之间的关系不再与基本过程的机制有关，在这种情况下发射和吸收之间的关系可以从宏观的热力学平衡定律，如由基尔霍夫定律求得，在一般情况下处理平衡态的辐射大都认为满足局部热力学平衡条件，如求算发射系数和吸收系数之间的关系就是基于局部热力学平衡条件得到的2

特征1、体系具有统一的温度，即Tg=Texc=Te=Tion=T，这里Tg是气体动力学温度，也是分子温度、离解温度，Texc是激发温度，Tion是电离温度，Te是电子温度； 2.分子的离解服从质量作用定律：MX=M+X

3.原子电离服从Saha热电离方程：M+e=M++2e

4.原子或离子的激发服从Boltzmann方程；

5.辐射服从Planck辐射定律。

局部热力学平衡状态下的等离子体电导率电导率理论模型水中放电等离子体的电导率由电子与周围介质的碰撞过程决定。理想条件下，等离子体完全电离，电子运动取决于电子与离子的库仑相互作用。最简单适用于理想状态下的等离子体电导率模型是Spitzer公式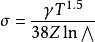（1）式中，为电子间碰撞对电导率的修正系数，T为温度，Z为离子的平均电荷数，为库仑对数，采用下式表示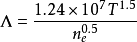：（2）在非理想条件下，电子与离子、电子与中性粒子的碰撞都会影响电子运动。Spitzer公式不适用于非理想条件下的电导率计算。因此，Z&L模型在Spitzer公式的基础上，对库仑对数进行修正，并采用较为合适的德拜屏蔽半径，得到适用于非理想条件下的电导率公式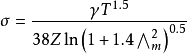： (3) 式中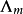，为修正后的库仑对数，采用下式表示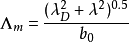： （4）式中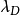，为德拜半径。

高温情况下，电子波的因素不容忽略，当电子通过圆孔时，将发生小角衍射，若该衍射角超过了经典散射角，将会增加散射导致的远距离碰撞。 因而将Z&L模型与量子机理作用相结合，得到的考虑电子与离子碰撞作用的电导率如下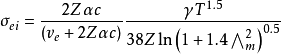： (5) 其中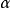，为精细结构常数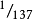，c为光速。考虑电子与中性粒子的碰撞作用下的电导率如下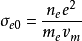： (6) 式中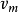，为电子与中性粒子动量传输过程中的平均碰撞频率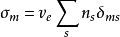，。其中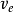，为电子平均热速度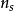，。为第s种中性粒子的数密度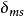，为电子与第s种中性粒子的动量传输碰撞截面。

综合（5）、（6）两式，非理想区域的电导率可通过下式表示：。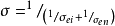

模拟计算及分析对电导率进行模拟计算前先做如下假设：

（1）水中等离子体处于局部热力学平衡状态；

（2）由于水分子、氧分子、氢分子、臭氧和多种自由基等粒子的含量较少，因而在计算中忽略以上粒子的作用；

（3）水的电离度较低，因而可以忽略氧原子二次以上的电离。

粒子数密度由电导率计算模型可知，为了模拟计算等离子体电导率随温度变化的过程，还需要知道各粒子密度和压力的数值。由假设可知水中等离子体处于局部热力学平衡状态，满足理想气体状态方程PV=nRT。同时，等离子体的粒子分布满足萨哈方程： （8）式中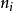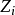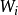，、、分别为粒子数密度、配分函数、电离势能。

电子数密度公式为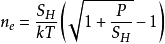： (9)式中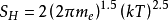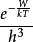，，P为压力，h为普朗克常数，W为电离能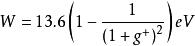，。其中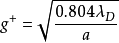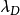，，为德拜半径，a为第一波尔轨道半径，大小为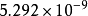m。

等离子体电导率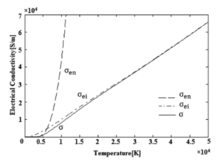将通过萨哈方程求得的粒子数密度代入电导率公式，可求相应的电导率数值。水中放电等离子体的粒子成分主要为电子、H原子、O原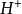子、离子、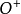离子，电子与H、O原子的碰撞截面近似取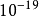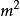，下图给出了考虑电子与中性粒子碰撞的电导率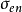、考虑电子与离子碰撞的电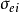导率及总电导率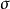随温度的变化趋势。

如图所示，总电导率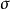随着温度T的升高而变大。考虑电子与中性粒子碰撞作用的电导率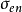，在较低的温度范围内随着温度的升高而变大。当温度接近10000K时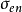，的增长速度突然变快。考虑电子与离子碰撞作用的电导率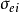，在一定范围内随着温度的升高而变大，且数值增大趋势渐缓。当温度高于25000K时，总导电率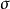几乎与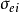重合。分析右图可知，温度较低时，电离度较低，电子与中性粒子的碰撞起主导作用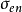，不可忽略，随着温度的升高，电离度增大，中性粒子数减少，从而电子与中性粒子的碰撞作用减弱，直至温度接近12000K时，电子与离子的碰撞作用逐渐增强。当温度高于25000K时，总电导率仅由考虑电子与离子碰撞作用的电导率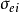决定33