简史
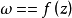 黎曼在他1851年的博士论文中陈述了这个结果,但其证明不完整。康斯坦丁·卡拉西奥多里在1912年发表了第一个完整证明。该定理是复变函数几何理论最基本、最重要的定理,是几何函数论的基础
黎曼在他1851年的博士论文中陈述了这个结果,但其证明不完整。康斯坦丁·卡拉西奥多里在1912年发表了第一个完整证明。该定理是复变函数几何理论最基本、最重要的定理,是几何函数论的基础
定理**(黎曼映射定理)**若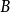 为单连通区域,其边界多于一点,
为单连通区域,其边界多于一点,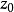 为
为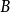 中任意一点,则在上存在唯一的一个一个把意义对应地映射成单位圆内部的共形映射
中任意一点,则在上存在唯一的一个一个把意义对应地映射成单位圆内部的共形映射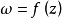 ,且
,且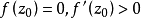 。
。
设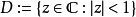 为开圆盘,
为开圆盘,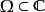 为单连通开子集。若
为单连通开子集。若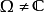 ,则存在一对一的全纯映射
,则存在一对一的全纯映射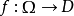 ,使
,使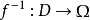 亦全纯。换言之,
亦全纯。换言之,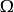 与
与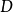 双全纯同构。
双全纯同构。
注意到二维的全纯映射不外乎保持定向的共形映射,它保持角度与定向不变。
注记1)黎曼映射定理乃是存在性定理,一般无法具体表示从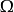 至
至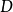 的全纯映射1。
的全纯映射1。
2)定理中对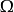 的条件极宽松;举例明之,
的条件极宽松;举例明之,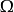 的边界可能是碎形曲线,但
的边界可能是碎形曲线,但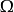 仍可透过共形映射映至单位圆盘,这在直观上是很难想像的。
仍可透过共形映射映至单位圆盘,这在直观上是很难想像的。
3)此定理对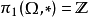 时即告失效:环型区域(形如
时即告失效:环型区域(形如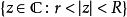 )之间的共形映射仅有反演、缩放与旋转。
)之间的共形映射仅有反演、缩放与旋转。
4)此定理在更高维度即不成立。
5)在黎曼曲面的框架下,此定理可推广为单值化定理:单连通黎曼曲面必同构于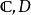 或
或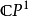 。
。
证明给定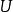 和
和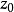 ,我们希望构造一个函数
,我们希望构造一个函数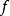 ,它把
,它把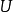 映射到单位圆盘,把
映射到单位圆盘,把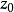 映射到
映射到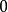 。在这个证明概要中,我们假设
。在这个证明概要中,我们假设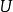 是有界的,且其边界是光滑的,就像黎曼所做的那样。记
是有界的,且其边界是光滑的,就像黎曼所做的那样。记
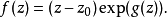 其中
其中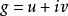 是某个(待确定的)全纯函数,其实数部分为
是某个(待确定的)全纯函数,其实数部分为 ,虚数部分为
,虚数部分为 。于是显然z0是f的唯一一个零点。我们要求对于
。于是显然z0是f的唯一一个零点。我们要求对于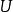 的边界上的
的边界上的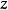 有
有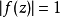 ,因此我们需要在边界上有
,因此我们需要在边界上有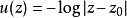 。由于
。由于 是全纯函数的实数部分,我们知道
是全纯函数的实数部分,我们知道 一定是一个调和函数,也就是说,它满足拉普拉斯方程。
一定是一个调和函数,也就是说,它满足拉普拉斯方程。
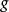 于是问题变为:存在某个实值调和函数
于是问题变为:存在某个实值调和函数 ,对所有的
,对所有的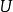 都有定义,且具有给定的边界条件吗?狄利克雷原理提供了肯定的答案。只要确立了u的存在,全纯函数的柯西-黎曼方程便允许了我们求出
都有定义,且具有给定的边界条件吗?狄利克雷原理提供了肯定的答案。只要确立了u的存在,全纯函数的柯西-黎曼方程便允许了我们求出 (这个论证依赖于
(这个论证依赖于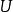 是单连通的假设)。一旦构造了
是单连通的假设)。一旦构造了 和
和 ,我们还需要验证所得到的函数
,我们还需要验证所得到的函数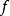 确实满足所有需要的性质2。
确实满足所有需要的性质2。
相关知识黎曼曲面
共形映射




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国