[科普中国]-费曼规则

定义

一般在计算有相互作用粒子散射、衰变的过程时，会将相互作用项看成微扰部分进行展开，为了方便写出每阶微扰的所有项而不重复或漏项，费曼提出了一种图形化来表达的方法，每一个费曼图代表一项。而费曼图中包含：外腿、顶点、传播子等部分，每一部分对应不同的数学表达式。图形与表达式之间的对应规则被称为费曼规则。

一般而言外腿、顶点、传播子对应相应的算式，按照费米子线相反的方向逐项写出，再对不确定动量进行积分、求迹（trace）运算，再乘上圈图提供的因子和对称因子就可以得到对应的费曼振幅12。

QED的费曼规则传播子部分如图1：

顶点部分如图2：

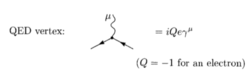
外腿部分如图3：

应用费曼规则在当今量子场论中是不可或缺的重要概念。费曼将图形化的语言引入到物理学具体的计算中也是理论物理界开创性的工作2。

在高能物理、粒子物理中，一般使用相对论性的场论，其费曼规则一般也就比较方便写成具有洛仑兹结构的普遍表达式。

在凝聚态物理中，一般使用非相对论性的场论，费曼规则往往对应着格林函数。而因为凝聚态方向相互作用项限制较小，具体问题不同也不一样，所以格林函数的具体形式往往也不一致。