定义
在做费曼图圈图计算时,总会出现为几个传播子分母乘积的整体因子1:

而在直接具体计算动量积分时十分麻烦,故而一般会想办法化为如下形式:
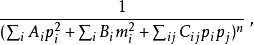 从而简化积分。这种简化计算的方法被称为费曼参数化。
从而简化积分。这种简化计算的方法被称为费曼参数化。
例如:
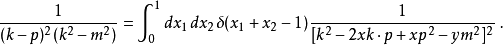 其中“
其中“ ”代表四矢量的缩并运算。
”代表四矢量的缩并运算。
公式最一般化的公式为1:
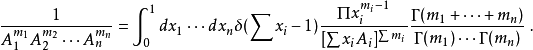 然而具体应用起来,简单的圈图计算不会用到这么复杂的形式,而是比较常用如下的几个公式:
然而具体应用起来,简单的圈图计算不会用到这么复杂的形式,而是比较常用如下的几个公式:
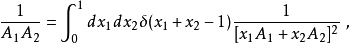
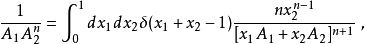
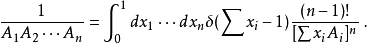
应用在使用维数正规化的方法来重整化,计算圈图时基本一定会用到费曼参数化2,可以说是量子场论中非常常用的公式之一。
定义
在做费曼图圈图计算时,总会出现为几个传播子分母乘积的整体因子1:

而在直接具体计算动量积分时十分麻烦,故而一般会想办法化为如下形式:
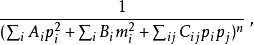 从而简化积分。这种简化计算的方法被称为费曼参数化。
从而简化积分。这种简化计算的方法被称为费曼参数化。
例如:
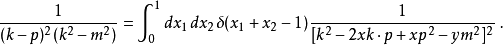 其中“
其中“ ”代表四矢量的缩并运算。
”代表四矢量的缩并运算。
公式最一般化的公式为1:
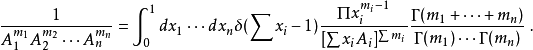 然而具体应用起来,简单的圈图计算不会用到这么复杂的形式,而是比较常用如下的几个公式:
然而具体应用起来,简单的圈图计算不会用到这么复杂的形式,而是比较常用如下的几个公式:
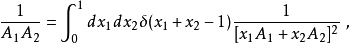
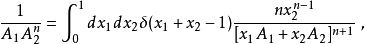
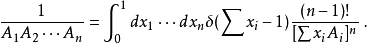
应用在使用维数正规化的方法来重整化,计算圈图时基本一定会用到费曼参数化2,可以说是量子场论中非常常用的公式之一。
 扫码下载APP
扫码下载APP

