[科普中国]-狄拉克代数

定义

首先我们定义狄拉克代数的基矢，也就是16个狄拉克矩阵（实际上在4维情况下狄拉克矩阵有多种表示，但狄拉克代数的性质与其具体表示的选取无关）12：

标量型矩阵：；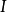

矢量型矩阵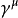：，共4个；

赝标量矩阵：；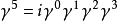

赝矢量矩阵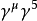：，共4个；

张量型矩阵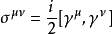：，共6个。

此外我们要求：

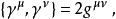其中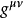为洛伦兹度规，也具有不同的取法。

通过如上定义，不难证明任一两个狄拉克矩阵的乘积可以表达为这16个狄拉克矩阵的线性组合。我们设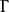为任一一种狄拉克矩阵的线性组合（有时也直接管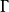叫狄拉克矩阵），那么两个任意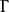矩阵的乘积也是16个狄拉克矩阵的线性组合。这样我们就定义了一个关于加法、乘法都封闭的代数结构。

性质加法满足交换律、结合律、对数乘的分配律1：

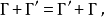
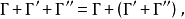
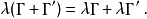乘法满足结合律、对加法的左、右分配律：

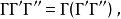
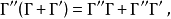
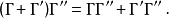此外还有：

应用狄拉克代数在描述狄拉克型费米子场时不可或缺，尤其是在构建诸如矢量流、赝矢流等的过程中。

标准模型中大部分的基本粒子是狄拉克型费米子，如夸克、轻子。它们的表述与相互作用的计算都离不开狄拉克代数。

此外在强子、介子衰变的研究中，也广泛应用狄拉克代数。