场的概念
若对全空间或其中某一区域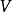 中的每一点
中的每一点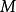 ,都有一个数量(或向量)与之对应,则称在
,都有一个数量(或向量)与之对应,则称在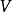 上给定了一个数量场(或向量场)。
上给定了一个数量场(或向量场)。
温度场和密度场都是数量场。在空间中引进了直角坐标系以后,空间中点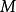 的位置可由坐标系确定。因此,给定了某个数量场就等于给定了一个数量函数
的位置可由坐标系确定。因此,给定了某个数量场就等于给定了一个数量函数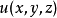 。在以下讨论中,假设
。在以下讨论中,假设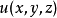 对每个变量都有连续偏导数。若这些偏导数不同时等于零,则满足方程
对每个变量都有连续偏导数。若这些偏导数不同时等于零,则满足方程
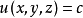 的所有的点通常是一个曲面,其中
的所有的点通常是一个曲面,其中 是常数。在这些曲面上函数
是常数。在这些曲面上函数 都取同一值,因此常称它为等值面。例如温度场中的等温面等。
都取同一值,因此常称它为等值面。例如温度场中的等温面等。
向量场可以重力场或速度场为例。当引进直角坐标系后,向量场就与向量函数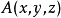 相对应。设
相对应。设 在三个坐标轴上的投影分别为
在三个坐标轴上的投影分别为
 则
则
 这里
这里 为所定义区域上的数量函数,并假定它们有连续偏导数。
为所定义区域上的数量函数,并假定它们有连续偏导数。
设 为向量场中的一条曲线。若
为向量场中的一条曲线。若 上每点
上每点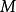 处的切线方向都与向量函数
处的切线方向都与向量函数 在该点的方向一致,即
在该点的方向一致,即
 则称曲线
则称曲线 为向量场
为向量场 的向量场线1。例如电力线、磁力线等都是向量场线。
的向量场线1。例如电力线、磁力线等都是向量场线。
需要注意,场的性质是它自己的属性,和坐标系的引进无关。引入或选择某种坐标系是为了便于通过数学方法来研究它的性质。
梯度场与方向导数(1)梯度场的概念由数量场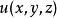 所得到的矢量场
所得到的矢量场
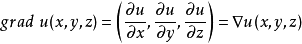 称为数量场
称为数量场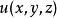 的梯度场2;对于定点
的梯度场2;对于定点 ,矢量
,矢量
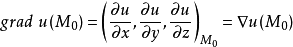 称为数量场
称为数量场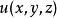 在点
在点 的梯度。
的梯度。
其中的算符
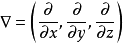 称为哈密顿算符,读作“Nabla”。
称为哈密顿算符,读作“Nabla”。
(2)方向导数① 定义1 设函数 在点
在点 的附近有定义,
的附近有定义,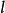 是从
是从 出发的射线,并设
出发的射线,并设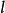 的单位方向矢量是
的单位方向矢量是 ,
,
 是
是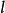 上任意一点。如果极限
上任意一点。如果极限
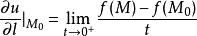 存在,则称这极限是函数
存在,则称这极限是函数 在点
在点 沿方向
沿方向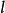 的方向导数。
的方向导数。
② 计算公式
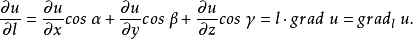 由此公式知:数量场的梯度刚好描述了数量场变化最大的方向和数值;所以,虽然梯度定义中用到了坐标系,但梯度这个矢量是和坐标系的选择无关的。
由此公式知:数量场的梯度刚好描述了数量场变化最大的方向和数值;所以,虽然梯度定义中用到了坐标系,但梯度这个矢量是和坐标系的选择无关的。
梯度的基本性质1、若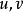 是数量函数,则
是数量函数,则

2、若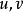 是数量函数,则
是数量函数,则
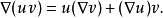 特别地有
特别地有

3、若 ,则
,则
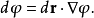
4、若 ,则
,则

5、若 ,则
,则

应用例1 设质量为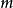 的质点位于原点,质量为
的质点位于原点,质量为 的质点位于
的质点位于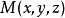 ,记
,记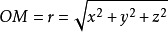 ,求
,求 的梯度。
的梯度。
解
 若以
若以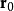 表示
表示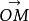 上的单位向量,则有
上的单位向量,则有
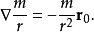
它表示两质点间的引力,方向朝着原点,大小是与质量的乘积成比例,与两点间的距离的平方成反比。这说明了引力场是数量函数 的梯度场。因此常称
的梯度场。因此常称 为引力势。
为引力势。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国