定义
设
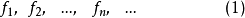 是一列定义在同一数集
是一列定义在同一数集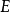 上的函数,称为定义在
上的函数,称为定义在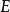 上的函数列。
上的函数列。
设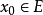 ,以
,以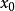 代入(1)可得数列
代入(1)可得数列
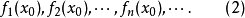 若数列(2)收敛,则称函数列(1)在点
若数列(2)收敛,则称函数列(1)在点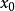 收敛,
收敛,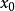 称为函数列(1)的收敛点。若数列(2)发散,则称函数列(1)在点
称为函数列(1)的收敛点。若数列(2)发散,则称函数列(1)在点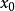 发散。若函数列(1)在数集
发散。若函数列(1)在数集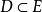 上每一点都收敛,则称(1)在数集
上每一点都收敛,则称(1)在数集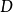 上收敛。这时
上收敛。这时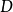 上每一点
上每一点 ,都有数列
,都有数列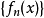 的一个极限值与之相对应,由这个对应法则所确定的
的一个极限值与之相对应,由这个对应法则所确定的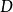 上的函数,称为(1)的**极限函数1。**若把此极限记作
上的函数,称为(1)的**极限函数1。**若把此极限记作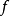 ,则有
,则有
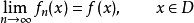 或
或
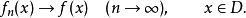
函数列极限的 定义是:对每一固定的
定义是:对每一固定的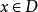 ,任给正数
,任给正数 ,恒存在正数
,恒存在正数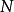 (注意:一般说来
(注意:一般说来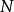 值的确定与
值的确定与 和
和 的值都有关,所以也用
的值都有关,所以也用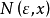 表示它们之间的依赖关系),使得当
表示它们之间的依赖关系),使得当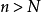 时,总有
时,总有
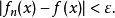 使函数列
使函数列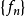 收敛的全体收敛点集合,称为函数列
收敛的全体收敛点集合,称为函数列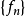 的收敛域。
的收敛域。
应用例1 设 为定义在
为定义在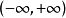 上的函数列,证明它的收敛域是
上的函数列,证明它的收敛域是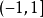 ,且有极限函数
,且有极限函数
 证 任给
证 任给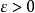 (不妨设
(不妨设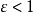 ),当
),当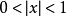 ,由于
,由于
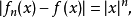 只要取
只要取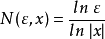 ,当
,当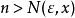 时,就有
时,就有
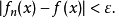 当
当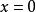 和
和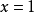 时,则对任何正整数
时,则对任何正整数 ,都有
,都有
 这就证得
这就证得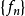 在
在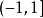 上收敛,且有(3)式所表示的极限函数。
上收敛,且有(3)式所表示的极限函数。
当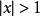 时,则有
时,则有 ,当
,当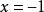 时,对应的数列为
时,对应的数列为
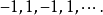 它显然是发散的. 所以函数列
它显然是发散的. 所以函数列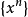 在区间
在区间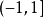 外都是发散的。
外都是发散的。
例 2 定义在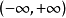 上的函数列
上的函数列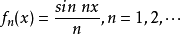 。 由于对任何实数
。 由于对任何实数 ,都有
,都有
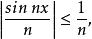 故对任给的
故对任给的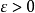 ,只要
,只要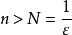 ,就有
,就有
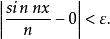 所以函数列
所以函数列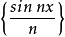 的收敛域为无限区间
的收敛域为无限区间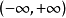 ,极限函数
,极限函数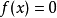 。
。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国