[科普中国]-流固耦合传热

基本概念

对于某些流体与固体之间的对流换热问题 ，热边界条件无法预先给定，而是受到流体与壁面之间相互作用的制约。这时无论界面上的温度还是热流密度都应看成是计算结果的一 部分，而不是 已知条件。像这类热边界条
件是由热量交换过程动态地加 以决定而不能预先规定的问题 ，称为流固耦合传热问题。2

用流固耦合传热方法可以将流体与固体之间复杂的外边界条件变成相对简单的内边界进行处理，不但减少了边界条件，又符合实际状态 从而提高了仿真的合理性和精度 。

解决方法对于耦合传热来说，热边界条件是由热量交换过程动态地加以决定而不能预先规定， 不能用常规的三类传热边界条件来概括。流体和固体边界上的热边界条件受到流体与壁面之间相互作用的制约 。这时无论界面上的温度是热流密度都应看成是计算结果的一部分，而不是已知条件 。

解决耦合问题的有效数值解法有顺序求解法和整场离散 、整场求解方法 。后者把不同区域中的热传递过程组合起来作为一个统一的换热过程来求解， 不同的区域采用通用控制方程，区别仅在于扩散系数及广义源项的不同。采用控制容积积分法来导出离散方程时，界面上的连续性条件原则上都能满足，省去了不同区域之间的反复迭代过程，使计算时间显著缩短，成为解决耦合传热问题的主导方法 。在流固耦合界面处，使用有限元软件提供的标准壁面函数法处理流动边界层和传热边界层。壁面函数法实际是一组半经验的公式，其基本思想是：对于湍流核心区的流动使用 k-ε模型求解， 而在壁面区不进行求解，直接使用半经验公式将壁面上的物理量与湍流核心区内的求解变量联系起来。这样，不需要对壁面区内的流动进行求解， 就可以直接得到与壁面相邻控制体积的节点变量值 。但是壁面函数法必须与高Re数 k-ε模型配合使用。
使用有限元软件进行仿真时，可根据所建立的仿真对象模型,设定不同零件各自的材料特性，流体的进出口边界及固体的外边界确定后直接施加在有限元模型上，并选定流固边界的计算条件———标准壁面函数法即可。

用数值仿真方法可以得到比试验测量更丰富的信息。虽然在流固耦合模型应用于数值仿真的初始阶段需要试验的验证，但是数值仿真依靠其数据丰富 、不受环境条件限制 、周期短 、成本低的优势，必将成为发展趋势 。
3

计算流固耦合传热计算 的关键是实现流体与固体边界上的热量传递。由能量守恒可知 ，在流固耦合的交界面 ，固体传出的热量应等于流体吸收的热量，因此 ，流固边界面上的热量传递过程可表示为 。式中： 为固体导热系数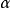； 为对流换热系数 ， 为固体壁面温度 ； 乃为流体温度。2

在求解流固耦合的瞬态温度场时，流体区域可按准稳态流场处理，即不考虑流场的动量和湍方程，则其控制方程式 ·( ρVφ) = ·( ΓVφ) + S 简化为仅包含温度变量，其他变量均视为定值，即 ·( ρVφ) = ·( ΓVφ) + S。

固体区域控制方程以其基本导热方程表示为 ，h 为显焓; λ 为导热系数; 为体积热源。等号左边第 1 项表示固体能量随时间的变化，右边 2 项分别表示传导引起的热流以及固内部的体积热源。对于各向异性导热的，其热传导项为 Δ·( λljΔT) ，λlj 为导热率张量。

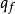流固交界面上不考虑发生的辐射、烧蚀相变等过程，则流固交界面上满足能量连续性条件，即温度和热流密度相等。具体控制方程式为 ， ，式中: 和 分别为流体温度和导热系数； 和 分别为固体温度和导热系数； 和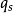 分别为流固交界面上流体侧和固体侧的热流密度； 为流固交界面法向量。

上述构成了流固耦合瞬态温度场控制方程，可以使用分区瞬态紧耦合算法进行求解。即在每个[t，t + Δt]时间步长内，完成如下计算步骤：

1) 假定耦合边界上的温度分布，作为流体区域的边界条件。

2) 对其中流体区域进行稳态求解，得出耦合边界上的局部热流密度和温度梯度，作为固体区域的边界条件。
3) 求解固体区域，得出耦合边界上新的温度分布，作为流体区域的边界条件。
4) 重复 2) 、3) 两步计算，直到收敛。1

相关研究紧耦合Stokos、Hooper、Kazemi-Kamyab等开发了将流体及固体内所有物理过程进行瞬态紧耦合算法，能使计算结果与实验结果高度吻合。但是，该瞬态紧耦合计算需要消耗大量的计算资源，难以用于解决实际复杂工程问题。

根据问题的特征，有些研究者近似认为在计算时间内，某些参数的状态是不变的，进而直接将瞬态问题转化为稳态问题。对于绝大多说不能通过准稳态处理直接转化为稳态问题的瞬态问题，有些研究者主张保留耦合的非稳态特性，提出各部分分别进行瞬态求解,并通过边界条件、参数值及活动网格等方式进行实时信息交互的瞬态松耦合传热问题的求解。如 Bauman 和Kazemi-Kamyab等针对高超声速流中固体表面带辐射及烧蚀相变过程的流固耦合强制对流传热问题，提出将流体 Navier-Stokes 方程与固体导热、辐射及烧蚀相变过程分别进行瞬态求解，并利用流体数值计算结果对其他求解方程的边界温度和热流加以修正，直至迭代收敛。Lohner 等针对飞机气弹分析中带固体形变的流固耦合传热问题，将流体 Navier-Stokes 方程及固体导热和应变方程分别求解，并利用流体数值计算结果对其他求解方程的边界温度和热流加以修正，同时利用固体应变方程的计算结果修正流体耦合边界位置和速度边界条件，直至迭代收敛。

松耦合有些研究者提出了基于准稳态流场的松耦合算法，即近似认为在整个流固耦合传热过程中，流场处于若干个准稳态，每一个准稳态的流场都使用稳态 Navier-Stokes 方程求解。如 Kontinos结合二维边界单元法和高超声速计算流体力学( CFD) 算法的松耦合算法，分析了高超声速流与机翼前缘的耦合传热问题。Chen 和Zhang等交替进行稳态流场计算与固体烧蚀和瞬态导热的松耦合算法计算了带烧蚀的流固耦合传热问题。