[科普中国]-动量表象

定义

每个物理态对应一个右矢量空间中的右矢量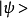 ，而这些右矢量可以用不同的完备基进行展开1：

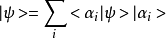而我们同样可以选取代表动量表象的完备基 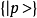，然后将一个物理态表述到动量空间**(注意：本节以及下一小节都选取的是一维动量空间，但做类似的简单推广就可以得到多维动量空间的结果)**：

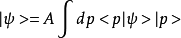其中A为一个归一化系数，不妨设为1。

其中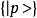 是动量算符的完备本征矢：

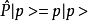
我们称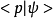 为该物理态的右矢量在动量表象中的表示。类似的，左矢量可以表示为 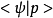，算符表示为 。

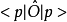性质对于一般性态矢量空间所满足的方程，都可以通过插入2：

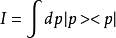进行改写，之后再利用归一化条件：

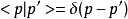把冗余的参量积分掉，就可以得到物理规律在动量表象对应的方程。

此外，动量表象下的物理规律与坐标表象只差一个傅立叶变换。

对于自由粒子而言：

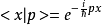
应用动量表象是所有表象中最常用的之一，因为动量是为数不多的比较易于实验测量的参数，而动量表象的物理意义就在于方便描述物理现象在动量空间的几率分布。

动量表象在非稳态问题中比较常用，尤其适用于散射理论。当今的粒子物理学基本上都是采用动量表象来进行表述。