[科普中国]-挡土墙稳定性

研究目的

挡土墙是一种用以抵挡土体坍塌的结构物。它在土建工程中的应用较广。如房屋建筑中的地下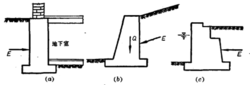室墙（图1-a），道路工程中支持边坡的墙（图1-b），桥梁中的桥台（图1-c）等。

就挡土墙结构的特点可分为重力挡土墙（图1）、薄壁挡土墙（图2-a）和板桩挡土墙（图2-b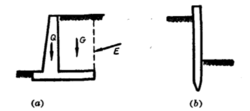）三种。

重力挡土墙截面的高度和宽度是同量极的，墙依靠本身的自重Q来抵抗墙后的土压力E，以维持平衡，这种挡土墙常用块石或混凝土砌筑而成。薄壁挡土墙普便是用钢筋混凝土板建造的，墙的自重Q虽不大，但是因为有水平板上的土重G的帮助，也足以抵抗土压力E。板桩挡土墙的截面高度较大而厚度很小，它是由木桩、钢筋混凝土桩或钢板桩所建造而成的，靠打入土内的深度来维持平衡。

作用于挡土墙上的土压力E确定后，即可进行挡土墙的设计。在设计时首先要使挡土墙具有足够的稳定性，以保证在土压力作用下不会绕边棱倾覆或沿墙底面滑动。3

对挡土墙稳定性的研究，包括安全系数验算和可靠度分析。

安全系数挡土墙的安全系数验算，通常包括抗倾覆稳定性和抗滑移稳定性验算。

抗倾覆稳定性验算图1（a）表示一具有倾斜基底的挡土墙，在墙重力和主动土压力的作用下可能绕墙趾O点向外倾覆，抗倾覆力矩与倾覆力矩之比称为抗倾覆安全系数Kt，应满足下列要求：

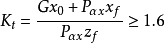
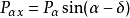
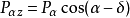
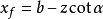
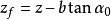
式中：

G——挡土墙每延米自重，kN/m；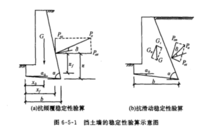

x0——挡土墙重心离墙趾的水平距离，m；

z——土压力作用点离墙趾的高度，m；

b——基底的水平投影宽度，m；

Pαx——主动土压力在水平方向的分量，kN/m；

Pαz——主动土压力在垂直方向的分量，kN/m；

α——挡土墙墙背与水平面的夹角，度；

α0——挡土墙基地的倾度，度；

δ——土对挡土墙墙背的摩擦角，由实验确定，也可以按表1选用。

当地基软弱时，在倾覆的同时，墙趾可能陷入土中，因而力矩中心O点向内移动，抗倾覆安全系数就将会降低，因此运用上式应注意地基土的压缩性。

|| || 表1 土对挡土墙墙背的摩擦角δ

注：φk为墙背填土的内摩擦角标准值。

抗滑动稳定性验算在土压力作用下，挡土墙有可能沿基础底面发生滑动（图1（b））。抗滑力与滑动力之比称为抗滑安全系数Ks，应满足下式要求：

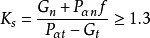
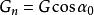
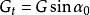
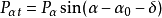
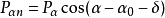
式中：

Pαt——主动土压力平行于基底面方向的分量，kN/m；

Pαn——主动土压力在垂直于基底面方向的分量，kN/m；

f——土对挡土墙基底的摩擦系数，由试验确定，也可以按表2选用。

|| || 表2 基础与地基的摩擦系数f

注：1.对易风化的软质岩和塑性指数Ip大于22的粘性土，基底摩擦系数应通过试验确定；

2.对碎石土，可根据其密实程度、填充物状况、风化程度等确定。1

模糊可靠度长期以来，挡土墙的设计均采用定值设计方法，以安全系数来表征挡土墙结构的稳定性程度。而事实上，在挡土墙稳定性分析中存在着大量的不确定性因素，主要包括随机不确定性和模糊不确定性。所谓事件的随机性，是指事件发生的条件不充分，使得在条件与事件之间不能出现必然的因果关系，从而事件的出现与否表现出不确定性。如土体的重度与内摩擦角等都可以看作是随机变量，而挡土墙的失稳可以看作是随机过程，可采用以可靠度理论为基础的设计方法来研究。

“模糊”是人们表达含糊的概念、观点和态度时使用的一个词。所谓模糊性是指边界不清楚，即在质上没有确切的含义，在量上没有明确的界限，是一种划分上的不确定性。模糊性产生的根源在于客观事物的差异存在着中间过渡，“亦此亦彼”的现象。例如，挡土墙的稳定性就是一个模糊概念，在失稳与稳定之间存在一个模糊过渡区。

可靠度分析在结构可靠度分析与设计中，为了正确描述结构的工作状态，必须明确规定结构安全、耐久、适用和结构失效的界限，这样的界限称为结构的极限状态。结构的极限状态实质上是结构工作状态的一个阈值，若超过这一阈值，则结构处于不安全、不耐久或不适用的状态；若没有超过这一阈值，则结构处于安全、耐久、适用的状态。如果用随机向量表示结构的基本随机变量X=(X1,X2,… ,Xn)，用g(°)表示描述结构工作状态的函数，称为结构功能函数，则结构的工作状态可用下式表示：

上式中：(1)失效状态；(2)极限状态；(3)可靠状态。

如果用R表示结构的抗力，用S表示结构上的作用（荷载）效应。则结构的功能函数可表示为：

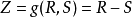
在挡土墙抗倾覆稳定性分析中，R为抗倾覆力矩，S为倾覆力矩。

在挡土墙抗滑稳定性分析中，R为抗滑力，S为滑动力。

在计算分析中，结构功能函数为非线性函数，若X1,X2,… ,Xn是结构中n个相互独立的随机变量，其平均值为μXi(i= 1,2,… n)，标准差为σXi(i= 1,2,… n)。将功能函数Z= g(X1,X2,… ,Xn)在随机变量的平均值处展开为泰勒级数，即：

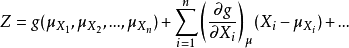
Z的平均值和方差可表示为：

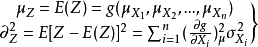
因此可靠度指标可表示为：

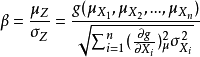
结构的失效概率可表示为：

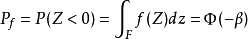
式中F表示结构的失效域，f(z)为结构功能函数的概率密度函数。

模糊可靠度计算由于事物本身存在着中间过渡现象及对事物划分标准边界的不清晰，一个元素只是在一定程度上属于一个集合，描述这种程度的就是模糊数学中的隶属函数。当考虑挡土墙由“完全失稳”到“完全稳定”之间的中介过渡性时，引入可以表征挡土墙稳定性的隶属函数μA(z)。

隶属函数的形式通常可以采用模糊统计试验的方法确定，或者从工程实际出发凭经验选取某一理论隶属函数，工程中常用的隶属函数的形式有半梯形分布、半正态分布、岭型分布等。

由于挡土墙的失稳既具有模糊性又具有随机性，为一模糊随机事件，根据模糊数学的理论，其发生的概率为：

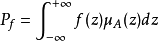
当μA表示失效程度时，μA接近于0时，失效的可能性小；当μA= 0.5时，处于最模糊状态，可作为传统分析时的极限平衡状态；当μA= 1时，失效的可能性大。当μA(z)采用降半梯形分布时：

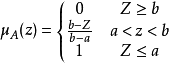
由于结构的功能函数具有随机性，可用其均值进行模拟。

挡土墙失稳的模糊可靠度为：4

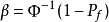
安全系数与可靠度关系①重力式挡土墙滑移失稳的机理比较简单，抗滑移原理明确，与重心位置无关，当截面积满足抗滑要求且不改变基底尺寸的情况下，加大墙顶宽度有利于抗倾覆稳定性的要求。

②可靠度指标随着对应安全系数的增大而增大，一直沿用的挡土墙验算方法定性分析是正确的，但可靠度指标与安全系数的数值关系不明确。得出一种工况下的数值关系，具有一定的参考价值，但尚需进一步计算其他工况下的数值关系以便得出具有概括性的函数关系。5