[科普中国]-自适应补偿

对于MIMO非线性系统执行器故障的容错控制问题已经有很多有效的方法被提出。其中，主动控制中的自适应补偿控制也是一种行之有效的方法。执行器故障自适应补偿控制是根据系统执行器的冗余情况，设计自适应补偿控制律，利用有效的执行器，达到跟踪参考模型运动的控制目的，同时保持较好的动态和稳态性能。自适应容错控制不需要FDD单元，在控制过程中跟踪控制律会随系统故障的发生而发生变动且自适应地进行重组。

因为自适应容错控制。可以同时解决故障和系统本身的不确定性的，且该方法不需要故障诊断和隔离单元，可以不受故障诊断误差的影响，同时也不会影响实时性，能够很好的处理故障引起的不确定性；不需要在系统故障时重新调整控制律的形式，结构简单；易于从理论上证明系统的稳定性和跟踪能力。所以得到了广泛的应用，并已经有不少的研究成果。1

工程中控制系统的传感器、执行器和控制对象等都不可避免地会发生故障，其中执行器由于长期频繁地执行任务，是系统中最易发生故障的部件。执行器故障会对系统的正常工作产生很大的影响，导致系统向无法预测的方向运行甚至使系统失去稳定性，所以执行器故障时的容错控制具有重要的理论意义和工程应用价值。容错控制涉及故障诊断与隔离、重构控制等技术，主要分为被动容错控制和主动容错控制两大类，主动容错控制相对于被动容错控制具有明显的优势，得到了广泛的研究。主动容错控制涉及的重构控制技术主要有线性二次型控制、多模型控制侧、模型参考控制、滑模控制和控制分配等方法，其中自适应补偿控制不需要故障诊断和隔离单元，可避免故障诊断误差的影响，且系统的实时性不会受到影响.基于这些优点，以Li等、Tao等、Wang等为代表的国内外学者对自适应补偿控制进行了广泛的研究和应用。2

其中有一篇文献为一类可全状态线性化的非线性系统设计了模糊自适应补偿律，但因其要求的非线性函数未知，故仅能解决有限的系统执行器故障跟踪控制问题；有的学者针对一类具有组合执行器故障的多输入单输出(Multi-input single-output,MISO)非线性最小相位系统设计了反演自适应补偿律，闭环系统能够稳定和渐近跟踪参考信号，且具有较好的动态性能；有的学者在以前的基础上将控制对象拓展为MIMO非线性最小相位系统，设计的控制律能使系统稳定且渐近跟踪参考信号。对系统执行器进行分组，以满足多种执行器故障组合的容错控制要求，是MIMO系统执行器故障容错控制设计相较MISO系统的主要难题之一，所以有学者对此问题进行了初步研究。采用执行器固定分组的方法，在控制律设计前将执行器分组完成，在系统运行时分组保持不变。因仅采用一种分组，故只能解决较少的执行器故障组合的容错控制问题。有的文献中采用了执行器虚拟分组方法，利用设计自适应律的方法在不同执行器分组之问选择，扩大了可补偿的执行器故障组合。但由于存在多个不确定参数相乘的情况，设计分组选择参数的自适应律较为复杂，且其仅考虑了执行器卡死故障，故不能适用其他类型的执行器故障。

自适应控制作为一种先进的控制方法，在飞行控制、卫星跟踪望远镜的控制、电力拖动、造纸等方面的控制中得到了成功的应用。然而，它在机械加工中的应用还不广泛。近年来，由于计算机技术的迅速发展，特别是微处理机的广泛普及，为自适应控制在机械制造中的实际应用创造了有利条件。

自适应控制是指在被控系统工作过程中，系统本身能不断地检测被控变量(即系统输出变量)，根据系统的输入(控制变量)和输出数据建立系统数学模型(系统动力学模型)，综合模型参数和系统输出观测值与参考值在各离散点处的偏差方差最小的目标，即可求得新的输入控制变量。这样系统就能逐渐地自适应地进入最佳工作状态，而其输出被控变量也能逼近其理想参考值。

自适应控制的研究始于上世纪50年代，目前从理论研究和实际应用的角度看，比较成熟的自适应控制系统有两大类:参考模型自适应控制系统和具有被控对象数学模型在线辨识的自适应控制系统。具有被控对象数学模型在线辨识的自适应控制系统能根据被控对象的输入输出数据建立数学模型，不必了解每一具体影响因素对被控对象的影响，使得我们对系统的分析变得更加简单。图为具有被控对象数学模型在线辨识的自适应控制系统方块图。

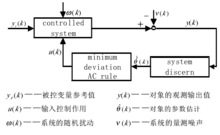
在图所示的自适应控制系统中，由系统输出的时间序列建立模型对系统进行辨识，最小方差自适应控制律利用辨识得到的参数进行综合运算，产生新的输入变量取代模型参考输入值经过不断的辨识，系统的模型会越来越准确，越来越接近于实际，基于这种模型综合出来的控制作用也将随之不断改进，最终系统的性能指标将渐近地趋于最优，系统的输出也会趋近于参考值。

由上面的叙述我们知道，自适应控制依靠的先验知识少，只需要被控对象的输入输出数据就可以建立数学模型，这非常适合于加工机理复杂的加工系统。另外，自适应控制具有“自适应”的能力，当系统内部特性或外部扰动的变化幅度很大时，系统可以逐渐适应，并使系统的性能指标渐近地趋于最优，而此时常规反馈控制系统的性能指标不仅不可能保持最优，而且常常要大幅度下降，甚至会引起系统的不稳定。因此，自适应控制优于一般的控制方式。

根据自适应补偿的控制目的和采用的方法主要可分为三类：利用状态反馈进行状态跟踪(Using State Feedback for State Tracking, SFST)、利用状态反馈进行输出跟踪(Using State Feedback for Output Tracking, SFOT)和利用输出反馈进行输出跟踪(Using Output Feedback for Output Tracking, OFOT)，这三类方法对系统已知条件和状态的要求依次降低，控制的难度和复杂程度依次增大。

SFST自适应补偿控制是通过设计自适应状态反馈控制律，以使系统在执行器故障情况下，其状态仍能够跟踪参考模型的状态。SFST自适应补偿控制研究的关键问题在于故障引起的不确定性、系统匹配条件和系统渐近跟踪性能等的处理。经过10余年的研究，SFST自适应补偿控制对于线性系统控制的基本问题已解决，对于非线性系统的控制仍在发展研究中。这种方法的主要缺点是对系统模型、状态、故障类型等需要满足的匹配条件过于严格，以至于相关研究结论的适用范围较小。

OFOT自适应补偿控制是通过设计自适应静态或动态输出反馈控制律，以使系统在执行器故障情况下，其输出仍能够跟踪参考模型的输出。这种方法的控制律需要更多的设计参数，并对系统的可观测性进行限制，而所设计控制律的性能也需要较强的匹配条件才能保证。OFOT自适应补偿控制的研究，由于需要讨论系统模型匹配条件、观测器存在和设计匹配条件等限制条件，无论对于线性还是非线性系统，研究成果都还不够丰富。

SFOT自适应补偿是通过设计自适应状态反馈控制律，以使系统在执行器故障情况下，其输出仍能够跟踪参考模型的输出。这种方法相对于SFST自适应补偿控制放宽了对系统状态、模型等匹配条件的限制，但由于减少了对系统已知信息的要求和需要考虑系统状态与输出的关系，增加了系统控制律的设计难度。由于多数工程系统需要进行状态反馈输出跟踪控制，故这种容错控制方法得到了广泛的研究。针对线性系统的执行器故障SFOT自适应补偿控制，G.Tao等对模型未知的线性时不变系统的执行器卡死故障进行了研究，讨论了与参考模型的匹配条件和自适应控制设计方法，但仿真表明故障发生后一段时间内系统的跟踪误差较大；在以后的研究中X. D. Tang等针对这类系统改进了控制算法，逐步达到了较好的控制效果。

S. H.Chen等将对线性系统的研究扩展到了非最小相位线性系统，但仅对系统需要满足的匹配条件进行了讨论，没有后续的研究结果。X. D. Tang等将该方法的研究扩展到了非线性系统，用Backstepping控制策略解决了一类非线性多输入单输出(Multi-Input Single-Output MISO)严反馈最小相位系统执行器卡死故障时的输出跟踪问题，但要求系统模型满足较为苛刻的严反馈和相对阶条件。G. H. Yang针对一类可全状态反馈线性化的MISO非线性系统，用模糊自适应控制方法完成了执行器卡死和部分失效故障的跟踪控制，但同时该方法要求系统非线性特性未知，故只能解决很少一类系统的有界跟踪控制问题。相对于MISO系统，MIMO系统由于输入输出的耦合和系统本身的复杂性，其控制问题难度更大。X. D. Tang等分别基于系统执行器满足的数学条件，对MIMO系统的执行器进行分组，对严反馈系统的SFOT容错控制进行研究，实现了对参考系统的渐近跟踪。但执行器的分类方法只适用于特定的系统类型，同时对系统模型的要求也较为严格。这些只是针对MIMO系统的初步研究结果，其限制条件和性能都有待更深入的研究。另外，现有成果对执行器故障的研究也往往限于卡死、部分失效等简单故障。3

3史密斯预估补偿方案的主要缺点是当预估模型与实际对象模型有偏差时，控制质量不理想，差异较大时会造成系统不稳定。当对象存在非线性时，因不同工作点的静态放大系数不同，所以当工作点变化时，原设汁的预估器的放大系数与实际值不同，系统则得不到完全的补偿，其动态过程的品质将受到影响。由于史密斯方案对预估模型误差，特别对增益误差十分敏感，所以1977年贾尔斯和巴特利提出了增益门适应方案，如图所示。即在业密斯预估模型之外加了除法器、比例微分环节和乘法器。除法器是将过程的输出值除以模型的输出值。比例微分环节中的

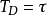
将过程输出与模型输出之比及其变化趋势送入乘法器。乘法器将预估器的输出乘以比例微分环节的输出，然后送到调节器。这三个环节的作用是模型和过程输出信号间的差值提供一个自动校正预沽器增益的信号。

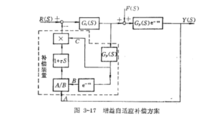
在理想情况下，预估器模型准确地复现过程输出，如图系统中，除法器输出值力1，得下图所示的等效框图。这相当于正反馈回路中只有预估模型的史密斯方案，纯滞后已经有效地被排除在闭环回路之外。但理想情况较少，多数情况下，模型输出和过程输出并不完全相同。此时，增益自适应补偿方案为一较复杂的控制系统，如图所示。

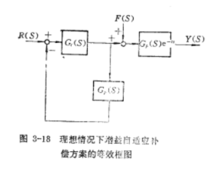
若广义对象的放大系数由Kp增加到Kp+△K，则必须使预占器模型的放大系数也增加到Kp+△K，才有可能得到理想控制。按图的方案，若Kp增加到Kp+△K； 则

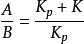
若不考虑识别器的作用，识别器输出也是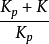，此值与Gp(S)的输出C相乘后，输入调节器作为反馈这，使反馈量也相应增加，S起超前补偿作用，获得一个识别变化趋势和变化方向的信号。若△K为正，并随时间增大，则起超前补偿作用，输出正的附加补偿量。当广义对象纯滞后改变时，通过比值的改变和识别器的作用，也可得到部分补偿。所以补偿装置；相当于变增益环节，系统等效框图如图所示。变增益环节中，增益Kp的大小取决于对象特性与预估器模型特性之差。Kp的最大值用限幅器加以限制。

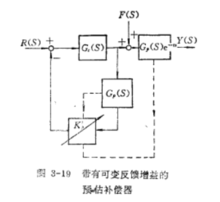
贾尔斯和巴特利进行了大量的数字竹真和摸拟实验研究，模拟二阶纯滞后的过程。从实验得出结论：增益自适应在负荷扰动对比于史密斯方案，而在给定值变化时，史密斯方案略优于增益自适应方案。

相对于对线性系统，非线性系统容错控制的研究广度和研究深度都需要进一步拓展。目前针对MISO系统的研究较多，但要推广到MIMO系统仍有许多问题需要解决；现有多数研究成果关注跟踪控制系统的稳定性和稳态性能，而对于所设计控制律的动态性能较少讨论，对于某些控制系统而言没有好的动态性能的控制律没有实际意义；在实际系统中往往存在不确定项，如外部干扰、建模误差等，不确定项会影响控制器的控制效果甚至使系统失去稳定性，由于执行器故障本身的未知性，使得考虑不确定项的执行器故障容错控制设计具有更大的难度；常见的执行器故障有卡死、部分失效和失效故障，在执行器故障容错控制中，要考虑单执行器的故障类型和多执行器的组合故障类型，现有的研究成果中大多考虑单个执行器故障或者有限的执行器组合故障，无法全面地考虑到多执行器可能发生的故障情况。4