[科普中国]-自旋波函数

概念

通常情况下，波函数的形式为：

这是因为，通常自旋和轨道运动之间是有相互作用的，所以电子的自旋状态对轨道运动有影响。但是，当这种相互作用很小时，可以将其忽略 ，则φ1，φ2对(x,y,z)的依赖一样，即函数形式是相同的，此时φ可以写成如下形式：

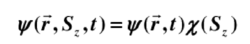
其中：

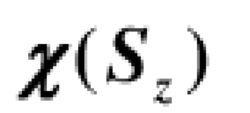
是：

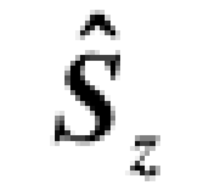
的本征函数，称为自旋波函数。

量子力学量子力学是研究微观粒子运动规律的理论，是现代物理学的理论基础之一。量子力学是在本世纪20年代中期建立起来的。19世纪末，人们发现大量的物理实验事实不能再用经典物理学中能量是完全连续性的理论来解释。1900年，德国物理学家普朗克提出了能量子假说，用量子化即能量具有的不连续性，解释了黑体辐射能量分布问题。1905年，爱因斯坦在此基础上提出了光量子假说，第一次揭示出光具有波粒二象性，成功地解释了光电效应问题。1906年，爱因斯坦又用量子理论解决了低温固体比热问题。接着，丹麦物理学家玻尔提出了解释原子光谱线的原子结构的量子论，并经德国物理学家索末菲等人所修正和推广。1924年，德国物理学家德布罗意在爱因斯坦光量子假说启示下，提出了物质波假说，指出一切实物粒子也同光一样都具有波粒二象性。1925年，德国物理学家海森堡和玻恩、约尔丹以矩阵的数学形式描述微观粒子的运动规律，建立了矩阵力学。接着，奥地利物理学家薛定谔以波动方程的形式描述微观粒子的运动规律，建立了波动力学。不久，薛定谔证明，这两种力学完全等效，这就是今天的量子力学。量子力学用波函数描写微观粒子的运动状态，以薛定谔方程确定波函数的变化规律。应用量子力学的方法解决原子分子范围内的问题时，得出了与实验相符的结果;量子力学用于宏观物体或质量、能量相当大的粒子时，也能得出与经典力学一样的结论。因此，量子力学的建立大大促进了原子物理、固体物理和原子核物理学的发展，并推动了半导体、激光和超导等新技术的应用。它标志着人类认识已从宏观领域深入到微观领域。量子力学为哲学研究的发展开辟了新的领域，它向人们提出了一系列新的哲学课题，诸如微观客体的存在特征、微观世界是否存在因果关系、主客体在原则上是否不可分、主客体之间的互补问题等等。深入和正确地回答这些问题，无疑将会推动马克思主义哲学的深入发展。1

自旋古典意义中的自转，是物体对于其质心的旋转，比如地球每日的自转是顺着一个通过地心的极轴所作的转动。在量子力学中，自旋是粒子所具有的内禀角动量引起的。

虽然有时会与古典力学中的自转相类比，但实际上本质是迥异的。自旋的发现，首先出现在碱金属元素的发射光谱课题中。

首先对基本粒子提出自转与相应角动量概念的是1925年由 Ralph Kronig 、George Uhlenbeck 与 Samuel Goudsmit 三人所为。然而尔后在量子力学中，透过理论以及实验验证发现基本粒子可视为是不可分割的点粒子，是故物体自转无法直接套用到自旋角动量上来，因此仅能将自旋视为一种内在性质，为粒子与生俱来带有的一种角动量，并且其量值是量子化的，无法被改变（但自旋角动量的指向可以透过操作来改变）。

自旋对原子尺度的系统格外重要，诸如单一原子、质子、电子甚至是光子，都带有正半奇数（1/2、3/2等等）或非负整数（0、1、2）的自旋；半整数自旋的粒子被称为费米子（如电子），整数的则称为玻色子（如光子）。复合粒子也带有自旋，其由组成粒子（可能是基本粒子）之自旋透过加法所得；例如质子的自旋可以从夸克和胶子的自旋得到。

自旋角动量是系统的一个可观测量，它在空间中的三个分量和轨道角动量一样满足相同的对易关系。每个粒子都具有特有的自旋。粒子自旋角动量遵从角动量的普遍规律，p=[J（J+1）]0.5h，为自旋角动量量子数，J = 0，1 / 2 ， 1，3/2，……。

自旋为半奇数的粒子称为费米子，服从费米 -狄拉克统计；自旋为0或正整数的粒子称为玻色子，服从玻色-爱因斯坦统计 。复合粒子的自旋是其内部各组成部分之间相对轨道角动量和各组成部分自旋的向量和，即按量子力学中角动量相加法则求和。已发现的粒子中，自旋为整数的，最大自旋为4；自旋为半奇数的，最大自旋为3/2。2

自旋是微观粒子的一种性质。自旋为0的粒子从各个方向看都一样，就像一个点。自旋为1的粒子在旋转360度後看起来一样。自旋为2的粒子旋转180度，自旋为1/2的粒子必须旋转2圈才会一样。 自旋为1/2的粒子组成宇宙的一切，而自旋为0，1，2的粒子产生物质体之间的力。自旋为半整数的费米子都服从泡利不相容原理，而玻色子都不遵从泡利原理。

波函数波函数是量子力学描写微观系统状态 (又称量子态或态) 的函数。是量子力学基本原理之一，也是量子力学中最基本最重要的量。在经典力学中，用质点的位置和动量(或速度) 来描写宏观质点的运动状态，当坐标和动量确定之后，质点的其他力学量，如能量等也就随之确定了。量子力学中描写状态的方式则不同。由于微观粒子有波粒二象性，粒子的位置和动量不能同时有确定值，因而质点运动状态的经典描述方式不再适用，代之以波函数来描写微观系统的状态。波函数的物理意义和基本性质归纳起来是： (1) 如果不考虑粒子的自旋，波函数是坐标r和时间t的复函数，用符号ψ(r，t)表示。就坐标变量而言，独立变量的数目等于微观系统自由度数。例如，对于单粒子系统，独立变量数目为3; 对于N个粒子系统，独立变量数为3N。考虑微观粒子的自旋后描写状态的波函数除了有位置和时间变量外，还应有自旋变量sz，这时波函数应表为ψ(r，s2，t)。(2) 对波函数的物理意义，玻恩首先提出了与实验相符的统计解释： 波函数模的平方给出粒子在空间一点出现的概率。因此波函数所表示的波和机械波、电磁波不同，它不是某种振动的传播，而是代表一种概率分布。所以这种波也常被称之为概率波。如单粒子系统处于由波函数ψ(r，t)所描写的状态，则|ψ(r，t)|2dr代表时刻t、空间r点附近dV体积内找到粒子的概率。如果描写微观系统状态的波函数已知，则系统在该状态下的各种力学量如坐标r、动量P、角动量L等的平均值或取值的概率可由波函数得出。就是说通过波函数可以得到系统相应状态下的一切物理性质。显然系统的状态不同则相应的波函数也不同。(3) 波函数随时间变化所遵从的规律是薛定谔方程。处于具体条件下的微观系统的波函数，可由相应的薛定谔方程解出。(4)波函数ψ(r，t)不单要满足薛定谔方程，还必须满足以下条件： 波函数在变量变化的全部区域内必须满足连续、单值、有限条件和归一化条件： *(r，t)ψ(r，t)=1，这些条件称为波函数的标准条件。3