[科普中国]-自旋算符

简介

自旋角动量是电子的内禀属性，无经典对应，即不能象角动量一样写成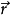 和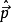 的函数，而是描述电子状态的又一个新的力学量。象其它力学量一样，自旋角动量也用一个算符表示。

利用角动量的定义： ；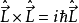

引入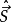 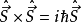： 。跟经典角动量的共性就是它们各自的对易关系一致。

自旋算符的对易关系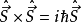

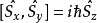
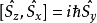
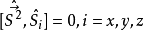
角动量平方算符：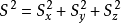

自旋算符的本征值由于在空间任何方向上的投影只能取两个数值，所以三个算符的本征值都是两个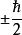 ，它们的平方就都是 ：

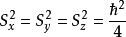
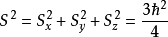
类似 ；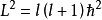

令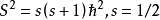

s与l相当，称s为自旋量子数。（l 叫轨道量子数或角量子数）。1

自旋算符的本征波函数本征：当我们仅研究自旋性质时，系统的空间部分波函数可以视为常数，选择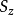 表象，则算符的两个本征态为：

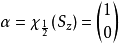
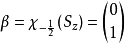
一般态：当体系自旋处在一般态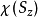 时，由前面基本假设，为自旋算符本征函数的线性组合，记为：

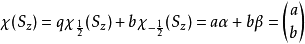
这样的列矩阵形式称为旋量，2行1列的矩阵二分量旋量，实际上也是二维Hilbert Space的一个矢量。

自旋算符的么正变换两种表象中的电子自旋算符的矩阵表示可以由两种表象之间的变换矩阵作么正变换相互转换。根据《量子力学》教科书中的有关论述，算符F 的态矢和矩阵表示从A表象到B表象的变换式分别为

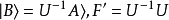
上式等价于：

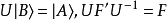
式中| B〉和F′为算符F 在B表象中的态矢和矩阵表示，| A〉和F为F 在A表象中的态矢和矩阵表示，U为从A表象到B表象的变换矩阵。虽然二者等价，但我们认为，为了使计算方便，选用第二个式子为表象之间的变换式更好。

以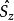从Sx表象到Sz表象的变换为例，设由Sx表象变换到Sz表象的变换矩阵为

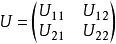
U必须为么正矩阵，即满足

可以计算得到由Sx表象到Sz表象的变换矩阵为

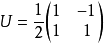
对电子自旋在Sx表象的表示作么正变换即可得到它们在Sz表象的表示，即对Sy表象的变换也可以作类似的讨论。2