[科普中国]-多变量广义预测控制

背景

预测控制作为一种有效的控制算法，已被大量的仿真和实际应用所证实。以前学者们对单变量的广义预测控制算法(CGPC)作了大量的研究，比如:单变量的MAC、DMC和GPC的算法，以及将单变量的广义预测控制应用到实际过程。工业过程通常为复杂的多输入多输出(MIMO)过程，近十年来，许多学者对于线性多变量广义预测控制进行了一些研究，并取得了一定的成果。如:关于基本的多变量单值广义预测控制算法的介绍，以及关于多变量广义预测控制和其解耦问题。广义预测控制作为一种优化控制算法，其优点之一就是可以直接处理多变量过程的控制问题。

一种多变量广义预测控制(MGPC)算法，它特有的隐式解耦功能可以有效地克服传统分散控制、解祸控制的烦琐和缺陷，并根据这个基本的算法提出一种将近似处理时滞的方法纳入广义预测控制的机制，可实现对各个通道的不同滞后时间的处理。由于广义预测控制应用于实际工程时，其算法较复杂，需要调整的参数较多，且在线计算时间较长，增加实际工程应用的复杂度，也不易于满足诸如电气传动这类快速系统的控制要求。

多变量控制多变量控制（Multivariable control）是指对多变量系统实现的控制。多变量系统（multivariable systems）是指具有多个输入量或输出量的系统，又称多输入多输出系统。

多变量控制系统必须要安装许多调节器及运算器才能进行控制，仅在某些特殊的情况下使用。

历来用模拟调节器进行控制时，除了对应一个控制变量选择一个操作变量以外，也可控制多个独立单环所组成的过程，从而对整个过程进行控制。但是生产过程在本质上是多变量系统，而且变量之间有种种影响。因此，在设计控制系统时，要尽可能避免互相影响。为了避免互相影响使控制性能变坏，对于有些即使本来需要控制的变量也宁可放弃而不控制。这样就不可避免地要出现所谓“失控”现象。例如，在蒸馏塔的控制系统中，对塔顶或塔底的任何一个组成部分进行自动控制时，就可以发现还存在有不能进行自动控制的“失控”等现象。

近年来，在化工生产过程中，设备间的互相影响正在显著增加。因此，一个操作变量会影响到许多控制变量。再有，一个控制变量也能支配受许多操作变量影响的，作为多变量系统的整个控制过程。想要在控制过程中消除影响，必须同时把许多变量综合起来加以控制，这样的控制方式，就是多变量控制。

在以前，多变量控制系统必须要安装许多调节器及运算器才能进行控制，仅在某些特殊的情况下使用。但是，随着DDC直接数字控制系统的普及，多变量控制系统实现起来也就更加经济了。

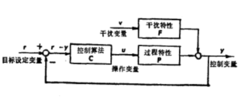
简介具有一个以上输入或一个以上输出的系统，在那里任一输入的变动产生来自一个以上输出的一个响应，叫做多变量系统。一般说来，会有m个输入和l个输出，如图所示。如果了l=m，这系统叫做方形系统。

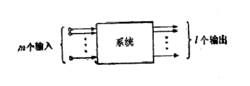
如果任一输入的变动产生来自一个以上输出的一个响应，那么这是由于系统中某种内部耦合或传输通路引起的，通常，当处理一个特定输入时，一个特定的系统输出端会比其他输出端起更大的响应，其他输出端对这个物入变动的响应叫做交互作用。

各个方面都出现多变量系统，例如电气，机械和化学工程，经济，医学工程，管理系统和环境系统.(来自热力学领域的)多变量系统的一个例子是汽车用双轴式气轮机.它有一组装在功率锅轮机进气端的可变几何形状的喷嘴，如图中的方框示意图所示，这个系统具有燃料流量、功率涡轮机喷嘴角度两个独立输入和必须控制的燃气发生器速度、功率涡轮机进气口温度两个输出变量。操纵任何一个输入都产生两个输出的变化。

优点同单变量系统相比，多变量系统的控制复杂得多。

多变量系统（multivariable systems）是指具有多个输入量或输出量的系统，又称多输入多输出系统。

在多变量控制系统中，被控对象、测量元件、控制器和执行元件都可能具有一个以上的输入变量或一个以上的输出变量。例如汽轮机的蒸汽压力和转速控制，石油化工生产中精馏塔的塔顶温度和塔底温度控制，涡轮螺旋桨发动机转速和涡轮进气温度的控制等，都是多变量系统的控制问题。多变量系统不同于单变量系统，它的每个输出量通常都同时受到几个输入量的控制和影响，这种现象称为耦合或交叉影响。交叉影响的存在使多变量系统很可能成为一种条件稳定系统。例如，在调试或运行过程中若增益发生变化或某一元件（例如传感器）断开或失灵，就可能导致不稳定。这是多变量系统特有的问题。在多变量控制系统的设计中，对于交叉影响的处理，常采用两种方式：①通过引入适当的附加控制器，实现一个输入只控制一个输出，称为解耦控制（见解耦控制问题）；②协调各个输入和输出间的关系，使耦合的存在有利于改善系统的控制性能，称为协调控制。此外，也可采用其他形式的指标来设计多变量系统的控制器。（见线性系统理论）

优点:

1)集中控制便于维护

2)由表头到单表头降低数据误差

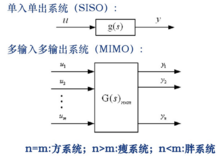
多变量系统的结构特点如图所示：

广义预测控制广义预测控制技术最初由Clarke和其合作者于1987年提出，它采用传统的参数模型(如CARIMA模型)，参数的数目较少，对于过程参数慢时变的系统，易于在线估计参数。由于引入了不相等的预测水平和控制水平，具有预测模型、滚动优化和反馈校正三个基本特征，呈现了优良的控制性能，被认为是具有代表性的预测控制算法之一，受到学术和工程界的广泛关注。但是基本的广义预测控制需要进行矩阵求逆运算，计算量很大，不适合要求快速响应的实时控制系统。

广义预测控制(GPC)具有预测模型、滚动优化和反馈校正等基本特征，呈现出优良的控制性能和鲁棒性，已广泛应用于工业过程控制。目前 GPC算法可分为间接算法和直接算法。

间接算法通过辨识被控对象的参数, 进行多步预测和在线滚动优化来设计控制律, 其缺点是需要求解逆矩阵。计算量很大。为此，在性能指标中引入下三角加权矩阵, 以避免矩阵求逆, 减少了计算量。根据待求逆矩阵中元素排列的特殊性进行矩阵分解, 并给出递推求逆算法, 将计算量减少了 2/3。

直接算法则根据某种规律直接辨识控制器的参数, 避免了在线求逆。通过引入等价性能指标, 先采用最小二乘法辨识被控对象的参数得到广义输出, 然后再辨识控制器参数, 并给出一种隐式 GPC 算法。

算法的改进采用其它数学预测模型的 GPC算法通过不同的数学模型可从不同的角度研究系统的特性。 GPC最初是基于 CARIM A模型推导的，CARIM A模型固有的积分作用有助于消除系统的静态偏差；许多学者将GPC推广到其它的预测模型 ，如CARMA模型、状态空间模型等等。应用预测模型推导了 GPC算法 在辨识之前先对数据进行特殊的滤波处理，以消除外界的突然干扰 ，并克服高速采样频率的作用。由于状态空间有利于控制系统的稳定性分析，一些学者从状态空间的角度研究了预测控制算法；将时域与频域相结合 ，使系统在时域上有较大的稳定裕度 ，通过加权多步预测得出稳定裕度的定量结果 ，利用频域特性拟合得出系统的降阶模型 ，提出了适用于降阶模型的多步预测控制算法；利用离散 Laguerre函数的性质建立对象的非结构模型 ，提出了一种非结构模型的广义预测控制器；采用优化方法确定对象的近似特征序列，提出了特征结构下的预测控制算法和相应的闭环反馈结构；则利用误差的历史数据来建立误差的预测模型，以误差预测补充模型预测 ，给出了基于误差预测修正的GPC算法.这些研究为我们从不同的角度研究和分析广义预测控制系统创造了条件。1

在线算法的改进在实际应用中，由于被控对象的时变、非线性、外界干扰等因素的影响，对象的参数往往很难精确得到，因此在实施GPC算法时，需要在线估计控制对象的参数，用于设计控制器。由于GPC算法中控制增量的计算涉及到矩阵求逆，因而在线计算量相当大。一些学者针对这一问题进行了研究，来减少算法的计算量。在提出 GPC算法时，给出了递推求解 Diophantine方程的方法；利用参数辨识的结果直接求解控制器，不用求解 Diophantine方程 ,减少了计算量；采用递推的方法建立预测模型，避免了求解 Diophantine方程，且算法不受多项式稳定的限制；袁著祉老师提出的递推广义预测控制器中给出了逆矩阵的递推算法，减少了计算量，同时该文还采用递推平方根法取代最小二乘法估计参数，改善了估计精度；根据待求逆矩阵中元素排列的特殊性，给出了求解逆矩阵的递推算法，进一步减少了计算量，其求逆计算量仅为通常的增广矩阵法的 30 % ；还提出了在性能指标函数中引入特殊的下三角加权矩阵，避免求解逆矩阵的算法，但算法对加权下三角矩阵的选择有一定的要求，提出了并行结构分解的算法，提高了在线计算效率。这些算法都是从减少计算量的角度来改进算法 ,以进一步满足实时控制的需要。另一种节省在线计算时间的算法是并行算法。慕德俊等分别针对状态空间模型和输入输出模型，采用递推的方法 ，将 GPC化为解 Ric-cati方程 ,基于脉冲阵列结构，提出了参数辨识的并行方法，给出的 GPC并行算法的最小二乘估计中的计算可并行 ，计算中 i对 j 可并行，求解 Doiphantine方程中，E和 F的计算可并行；此外还有将辨识与控制分离的 GPC算法。.这些并行算法提高了 GPC的实时性，为 GPC的实际应用打下了理论基础。

广义预测极点配置控制算法为了保证闭环系统的稳定性，1987年，Lelic和 Tarrop结合极点配置算法，提出了广义极点配置自校正控制器 ，使闭环系统具有较好的控制性能；在性能指标函数中采用了加权系数，通过选择适当的加权系数来使闭环系统的极点配置在预先指定的位置，来改善系统的性能；通过在线选择加权项进行极点配置 ,避免 GPC的在线求逆；利用 GPC和极点配置，侧重系统的跟踪特性、自适应能力、降阶建模和鲁棒性，给出了广义预测极点配置的实际应用例子。

稳定广义预测控制算法稳定广义预测控制算法（Stable Generalized Predictive Control，SGPC）是由Kouvaritakis等提出的一种控制方法．该方法是针对广义预测控制（GPC）算法缺乏稳定性保证而提出的一种改进算法。SGPC首先通过引入一种反馈控制结构，以此来简化系统内部的某些关键变量之间的关系，然后通过优化目标函数找到参考时域内的最优参考信号序列，从而得到控制量的增量．该方法通过对未来参考信号的约束，间接实现了对未来系统输出的约束，进而保证系统的稳定性。2

与其它最优控制相结合的 GPC算法各种传统的控制方法以及优化控制都有其自身的优点，将这些算法与广义预测控制相结合，扬长避短，有助于进一步改善控制系统的特性.由于传统的 PID控制算法简单，易于实现，至今仍在大量的控制过程中得到广泛的应用。将PID算法与 GPC相结合的研究成果有采用了 PI型的性能指标的 PI型广义预测控制算法、炼油装置加热炉出口温度的 GPC-PID串级控制算法等；将神经网络、 PID和 GPC有机地结合在一起 ，提出了基于 BP网络的PID型预测控制器。神经网络在并行计算和处理非线性系统方面有其独特的优越性。将神经网络用于 GPC的研究成果有利用 Tank-Hopfield网络处理 GPC矩阵求逆的算法、基于神经网络误差修正的GPC算法、利用小脑模型进行提前计算的 GPC算法、基于 GPC的对角递归神经网络控制方法以及用神经网络处理约束情形的预测控制算法等。

控制系统的分析目前 GPC算法的稳定性和鲁棒性分析大多依赖于计算机仿真和实际控制其理论分析还相当缺乏，这是由于 GPC引入了多步预测和柔化作用以及 GPC算法本身的特殊性，使广义预测控制系统的分析相当复杂。目前的分析结果都是在一定的条件下得出的。

稳定性分析当预测模型没有建模误差时， Clarke等人从状态空间的角度对 GPC的稳定性进行了分析，认为当开环系统能稳可测时，通过选择适当的参数，可以使闭环系统在有限时域内稳定，并产生稳定的状态最小拍控制；当预测长度趋近无穷大时，闭环系统稳定，但算法的计算量将随预测长度的增加而呈指数倍增长，这就要求预测长度在适当的范围之内，因此在一般情形下， GPC算法并不一定能保证系统的闭环稳定性。针对这个问题，众多学者进行了大量的研究，有些学者通过对算法的改进来保证系统的闭环稳定性，如上节中提到的各种稳定的广义预测控制算法；还有一些学者则直接从理论上来分析 GPC的稳定性，这些分析主要有两类：基于内模控制原理和状态空间分析。3

基于内模控制原理

采用内模控制原理分析 GPC的稳定性以席裕庚等人为代表。将 GPC结构转换为内模结构，推导了控制器的表达式，认为 GPC系统的动态特性取决于控制器多项式的极点，GPC算法不改变系统的纯滞后或非最小相位特性；且当闭环系统稳定时， GPC可有效地抑制确定性的干扰；GPC最优控制的可解性，研究了系统闭环特性与设计参数的关系；给出了选择设计参数使 GPC闭环系统具有最小拍性质的结论，即在 p个周期后，系统的脉冲响应为 0，使系统 p拍后达到稳定；此外，席裕庚等人还分析了闭环系统的性质，讨论了闭环系统的阶次；并给出了根据阶跃响应来保证系统闭环稳定的参数设计条件。

状态空间分析

状态空间描述比较有利于系统的稳定性分析，在噪声强度不大和无结构型建模误差的条件下，GPC是一种性能优良、闭环稳定的算法，适用于阶次上界已知的对象，适用于时滞未知但上界已知的对象，适用于非最小相位系统，适用于能稳能测的开环不稳定系统，具有良好的跟踪和稳态性能，能抑制确定性干扰，优于极点配置、 LQG、广义最小方差控制器等算法；分析表明，若开环系统稳定，预测模型无偏差，则当预测长度足够大时，闭环系统稳定；分析了输入输出受限时的稳定性，给出了闭环稳定的条件；GPC增加的极点在 Z平面的原点上，在预测长度相同时，系统的稳定性与时滞无关；广义预测控制系统的状态空间结构，指出其实质是一种状态反馈，通过选择适当的控制器参数可以保证系统的闭环稳定性，指出闭环系统与开环系统有相同的阶次，它不改变系统的零点，但有助于克服纯滞后对系统闭环特性的影响；当系统时滞已知时，选择控制量加权系数为 0可保证最小相位系统闭环稳定，若参数摄动不改变系统的最小相位特性，则闭环系统鲁棒稳定。

鲁棒性分析鲁棒性是系统存在建模误差或摄动时的稳定性，目前对 GPC的鲁棒性分析成果包括最优性和稳定性的鲁棒性分析，有离散域和频域的。 Clarke对 GPC的鲁棒性作了简单的分析，但没有涉及到任意预测长度下的鲁棒性问题；GPC的强鲁棒性源于对系统建模误差的预测功能，认为若预测精度较高，预测时域长，则可改善 GPC的最优鲁棒性；同时GPC的稳定鲁棒性较经典的最优控制有了提高，它改善了系统的信噪比；采用输入输出模型，给出了保证 GPC鲁棒性的必要条件，认为噪声多项式是改善鲁棒性的重要因素；噪声滤波器对系统鲁棒性的影响，认为当模型无失配时，系统的稳定性与噪声多项式无关，当模型失配时，可通过选择噪声滤波器来改善系统的鲁棒性；对具有干扰、饱和输入和非线性未建模动态的系统进行了综合设计，给出了输入输出鲁棒稳定的充分条件减少反馈通道的增益有助于提高鲁棒性；根据小增益定理，从频域分析了系统的鲁棒性，给出了闭环系统鲁棒稳定的条件。4