[科普中国]-有限维重复控制

背景

针对一类具有严重非线性扰动的伺服系统，提出一种有限维重复控制万法以实现高精度的信号跟踪所考虑的扰动与系统输出间存在未知非线性关系，仅设其满足连续里普希斯条件，便可处理大多数实际情况应用不动点原理，给出了所提出万法有效的充分条件，该条件也是应用基于系统周期不变性的学习控制方法的必要条件在稳定的闭环系统中，利用H阶有限维重复控制器，可实现参考信号前H次谐波的渐近跟踪仿真结果证明了万法的有效性。

引言在伺服系统中，经常需要实现对周期外激励信号的高精度跟踪。例如，工业机器人在执行重复性操作时机械手臂的轨迹控制。在这类伺服系统中，由于机械结构上的非对称性或驱动机构的不完善，经常会引入一类与系统输出相关的非线性扰动，这类扰动通常难以处理且可能严重影响跟踪精度.通过改善机械结构或提高制造工艺来消除以上扰动，通常代价昂贵，甚至是不可能的.因此，有必要寻求一种简单、有效、低成本的扰动补偿控制方法。

在线性系统中，重复控制方法对于周期信号的跟踪或干扰抑制是十分有效的，但对于非线性系统，重复控制的研究结果还很有限。实际上，由于重复控制器中含有时滞正反馈回路，使得非线性重复控制系统的性能难以保证。为此，可以在应用重复控制方法前采用一些线性化技术，但这大大增加了系统设计和实现的复杂性。

基于降阶近似内模的思想的有限维重复控制方法，并将其应用于具有未知非线性输出相关扰动的伺服系统.对于扰动信号，仅设其满足连续里普希斯条件，这可以处理大多数实际情况。推导了有限维重复控制方法的应用条件，这些条件是其他基于系统周期不变性的学习控制方法得以应用的基础。理论分析和仿真结果表明，利用提出的H阶有限维重复控制器，可以完全消除稳态误差的前H次谐波，同时系统也获得了良好的暂态响应特性。

重复控制重复控制是日本的Inoue于1981年首先提出来的，用于伺服系统重复轨迹的高精度控制。重复控制之所以能够提高系统跟踪精度，其原理来源于内模原理。

加到被控对象的输入信号除偏差信号外，还叠加了一个“过去的控制偏差”，该偏差是上一个周期该时刻的控制偏差。把上一次运行时的偏差反映到现在，和“现在的偏差”一起加到被控对象进行控制，这种控制方式，偏差重复被使用，称为重复控制。经过几个周期的重复控制之后可以大大提高系统的跟踪精度，改善系统品质。这种控制方法不仅适用于跟踪周期性输入信号，也可以抑制周期性干扰。

原理在重复控制中，一般期望重复控制作用在高频段的增益减小。为此，在重复控制中经常加入低通滤波器

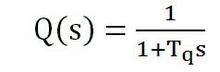
式中，Tq>0为滤波器的时间常数。

重复控制信号为周期性信号，其基本构造如图所示，r为周期参考信号。应用重复控制不仅可以提高系统的跟踪精度，还可以提高系统的鲁棒性。

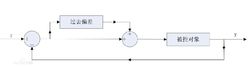
重复控制是基于内模原理的一种控制方法。所谓内模原理，即在一个闭环调节系统中，在其反馈回路中设置一个内部模型，使该内部模型能够很好地描述系统外部信号特性，通过该模型的作用可使系统获得理想的指令跟踪特性，具有较强的扰动抑制能力。内模原理的本质是将系统外部信号动态模型(即为内模)植入控制系统内以此来构成高精度的反馈控制系统，使系统能够无静差地跟随输入信号。

有限维重复控制详述重复控制是基于内模原理提出的。

内模原理指出：如果希望一个稳定的反馈系统实现对某一外激励信号的稳态无差跟踪或抑制，则其充分必要条件是在系统回路内设置这一信号的发生器。而对于周期性的外扰动，将在系统回路内设计一信号发生器，可以抑制周期扰动信号。这里选择时滞环节

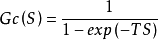
来做为内模模型，由于时滞环节在虚轴上有无穷多个极点。在闭环系统中设置这样一个环节，可以抑制周期为T的扰动信号。由分析可知，如在系统中引入这种形式的内模，则所能镇定的对象类型是十分有限的，即只有对象相对度为零时系统才是可镇定的。

因此产生了改进的重复控制方法，做为内模模型，Q(S)为低通滤波器以放宽稳定条件。在低频段Q(S)=1，因此Gcg(S)具有控制系统带宽内的低频近似虚极点，而带宽外的高频虚极点己经被滤除，决定系统性能的仅是在g(s)带宽内的有限个近似虚极点，另外从稳态性能来说，重复控制器所引入的无穷多个极点是不必要的，而这些极点对于系统的稳定性和暂态性能都是有影响的。因此采用与Gcg (S)达到同样效果的有限维重复控制环节，n阶次，可以根据周期扰动谐波的次数和所需要控制的精度来确定。

上述有限维重复控制环节仅适用于消除某一基波和其n次谐波的扰动信号，而转台的动不平衡是三个框架结构以不同的速率转动引起的，产生的为多个不同频率的周期扰动信号，因此改进有限维重复控制环节。多周期有限维重复控制器，用于消除存在多周期扰动信号的控制系统的误差。

有限维重复控制器在重复控制方法中，稳定闭环系统引入了形如

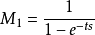
的外激励周期信号的完全内模M1，在虚轴上的无穷多个极点使系统可对任意周期为T的周期信号买现渐沂跟踪或抑制，但由于系统的稳定性很难保证，一般必须在时延环节前引入一个低通滤波器，即取近似内模

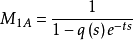
低通滤波器滤掉了高频虚极点，影响系统性能的只有低通滤波器带宽内的有限个近似虚极点。

另一方面，大多数实际信号的功率都集中在低频带。因此只需在闭环系统中放置包含重复频率主要谐波成分的近似内模，即可实现周期性外激励信号的高精度跟踪或抑制。由于只采用有限个谐波模型，使得系统易于镇定.基于以上概念，引入H阶有限维内模。

依据内模原理，跟踪误差不含有H阶和低于H阶的谐波成分，即可实现周期参考信号或干扰信号前H次谐波成分的稳态无差跟踪或抑制。

特别地，对于系统的稳态误差给出下列定理：

定理：设对图1所示非线性系统，当Cre(s)中包含形如H阶有限维内模MF且系统稳定时，系统的稳态误差不可能含有阶次小于或等于H的谐波成分，即

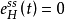
证明反证法：图1所示非线性系统的稳态误差是周期函数且有界。同样可知，闭环系统的所有解也是有界的.现假设跟踪误差中含有阶次为a(a