[科普中国]-相位补偿控制

基于不变性原理组成的自动控制称为补偿控制，它实现了系统对全部干扰或部分干扰的补偿。 按其结构的不同， 补偿控制系统一般有前馈控制系统和大迟延过程系统两种。补偿控制系统广泛应用于工业生产过程、医学、心理学、军事、电机、计算机等领域。

前馈控制是以不变性原理为理论基础的一种控制方法， 属开环控制系统。 常用的前馈控制系统有单纯前馈控制系统、前馈 -反馈控制系统和前馈 -串级控制系统等三种结构形式。大迟延系统的解决方法很多， 最简单的是利用常规控制器。主要采用常规 PID 的变形方案，如微分先行控制方案和中间微分控制方案等。

在供电电压全周或半周内，使电流开始流通的瞬时起变化的过程。在此过程中电流通过零值左右就停止。

通过控制触发脉冲的相位来控制直流输出电压大小，简称相控方式。1

例如：可控整流电路中，调节触发信号触发角a，可控制输出电压Ud的大小。对应的还有斩波控制、SPWM控制。

1. 改变反馈网络相移，补偿运放相位滞后
　　2. 补偿运放输入端电容的影响（其实最终还是补偿相位……）

因为我们所用的运放都不是理想的。

一般实际使用的运算放大器对一定频率的信号都有相应的相移作用，这样的信号反馈到输入端将使放大电路工作不稳定甚至发生振荡，为此必须加相应的电容予以一定的相位补偿。在运放内部一般内置有补偿电容，当然如果需要的话也可在电路中外加，至于其值取决于信号频率和电路特性 。

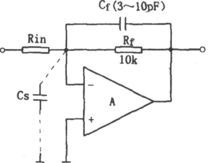
一般线性工作的放大器(即引入负反馈的放大电路)的输入寄生电容Cs会影响电路的稳定性，其补偿措施见图。放大器的输入端一般存在约几皮法的寄生电容Cs，这个电容包括运放的输入电容和布线分布电容，它与反馈电阻Rf组成一个滞后网络，引起输出电压相位滞后，当输入信号的频率很高时，Cs的旁路作用使放大器的高频响应变差，其频带的上限频率约为：

ωh=1/(2πRfCs)

若Rf的阻值较大，放大器的上限频率就将严重下降，同时Cs、Rf引入的附加滞后相位可能引起寄生振荡，因而会引起严重的稳定性问题。对此，一个简单的解决方法是减小Rf的阻值，使ωh高出实际应用的频率范围，但这种方法将使运算放大器的电压放大倍数下降(因Av=-Rf/Rin)。为了保持放大电路的电压放大倍数较高，更通用的方法是在Rf上并接一个补偿电容Cf，使RinCf网络与RfCs网络构成相位补偿。RinCf将引起输出电压相位超前，由于不能准确知道Cs的值，所以相位超前量与滞后量不可能得到完全补偿，一般是采用可变电容Cf，用实验和调整Cf的方法使附加相移最小。若Rf=10kΩ,Cf的典型值丝边3～10pF。对于电压跟随器而言，其Cf值可以稍大一些。

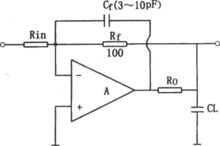
对于许多集成运算放大电路，若输出负载电容CL的值比100pF大很多，由于输出电容(包括寄生电容)与输出电阻将造成附加相移，这个附加相移的累加就可能产生寄生振荡，使放大器工作严重不稳定。解决这一问题的方法是在运放的输出端串联一个电阻Ro，使负载电容CL与放大电路相隔离，如图所示，在Ro的后面接反馈电阻Rf，这样可以补偿直流衰减，加反馈电容Cf会降低高频闭环电压放大倍数，Cf的选取方法是：使放大电路在单位增益频率fT时的容抗Xcf≤Rf/10，又Xf=l/(2πfTCf)，一般情况下，Ro=50～200Ω，Cf约为3～10pF。

除了上述不稳定因素之外，还存在其他一些不稳定因素，有些是来自集成芯片自身。有些是源于系统电路(例如电源的内阻抗的耦合问题)。有时使用很多方法都难以解决不稳定问题，但采用适当的补偿方法后可使问题迎刃而解。例如。当放大器不需要太宽的频带和最佳转换速率时，对集成运放采用过补偿的方法会取得很好的效果，如将补偿电容增加9倍或为实现稳定性所需要的倍数，对μA301型运放而言，其效果一般都较好。

设被控对象受到干扰 Di(t) 的作用时，被控变量 y(t)的不变性可表示为：当 Di(t)≠0 时，则 y(t)=0 (i=l,2,…,n) ，即被控变量 y(t)与干扰 Di(t) 独立无关。基于不变性原理组成的自动控制称为补偿控制， 它实现了系统对全部干扰或部分干扰的不变性，实质上是一种按照扰动进行补偿的开环系统。

补偿控制首先求出满足性能指标的控制规律，然后在系统中增加补偿控制器，来改变控制器的响应，从而使整个系统获得期望的性能指标。

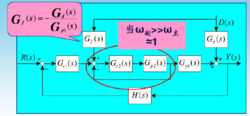
（1）按控制量补偿：将控制输入量R(S)经过处理(Gc(S))后，直接向前传递，并与主控制器的输出进行叠加。控制信号直接作用到被控对象，构成开环控制的补偿。

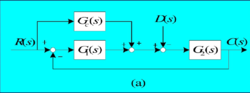
（2）按扰动量补偿：将系统的扰动输入量D(S)经过处理(Gc(S))后向前传递，与主控制器的输出进行叠加。增加扰动信号的前向通道，利用双通道原理来补偿干扰。

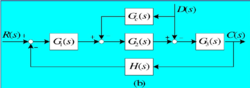
即反馈校正，在主控制器反馈回路中增加一个控制器。

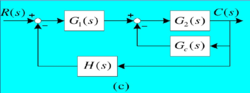
即串联校正，将补偿器与主控器串联起来。

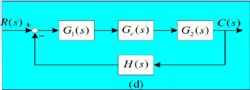
前馈控制是按扰动量的变化进行控制的，是一种扰动补偿或按扰动控制，是一种开环控制，如图1。

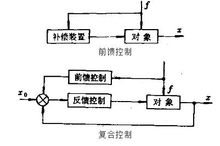
根据不变性原理(即扰动补偿原理)，要实现扰动补偿，就必须使用补偿装置，使扰动点与被控量之间具有两个通道，并且使与动态特性的大小相等，符号相反，才能实现完全补偿。如果两个通道仅放大系数相等，则仅能实现静态补偿。通常，前馈控制不单独使用，而是与反馈控制同时使用，即组成复合控制系统，同时按偏差与按扰动调节。

系统出现扰动时，立即将其测量出来，通过前馈控制器，根据扰动t的大小来改变控制量，抵消或减小扰动对被控量的影晌。被控量的偏差并不反馈到控制器，而是将系统的扰动信号前馈到控制器，故称前馈控制。

前馈控制是开环控制，在控制过程中不测取被控参量信息，只对指定的扰动量进行补偿；对指定的扰动量，由于数学模型的简化、工况的变化及对象特性的漂移，很难实现完全补偿；系统的干扰因素较多，若对所有的扰动进行测量井采用前馈控制，增加系统的复杂程度，而有些扰动量无法测量，不可能实现前馈控制。

在系统中引入前馈控制应遵循的原则：

（1）系统中的扰动量是可测不可控的。若干扰不可测，前馈控制无法实现。若干扰可控，可设置独立的控制系统予以克服。

（2）系统中的扰动量的变化幅值大、频率高。高频干扰对被控对象的影响很大，易导致持续振荡 。采用前馈控制，可以对干扰进行同步补偿控制，获得较好的控制品质。

（3）控制通道的滞后较大或干扰通道时间常数较小。

当被控对象的控制通道和干扰通道的传递 函数不同时，或对动态误差控制精度要求很高的场合，必须考虑采用动态前馈控制方式。

动态前镶控制的原理是：通过选择适当的前馈控制器，使干扰信号经前馈控制器至被控量通道的动态特性完全复制对象干扰通道的动态特性，但符号相反，以实现对干扰信号的完全补偿。动态前馈控制可使系统静态偏差等于或接近于零，又可使系统的动态偏差等于或接近于零。

前馈控制器用来消除主要扰动量的影响；反馈控制器则用来消除前馈控制器不精确和其它不可测干扰所产生的影响。

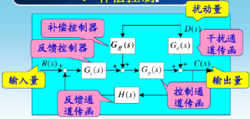
如果被控对象的主要干扰频繁而又剧烈，而生产过程对被控参量的精度要求有很高，可以考虑采用前馈一串级控制方案。

大延迟过程是指广义对象的时滞与时间常数之比大于0.5 。工业生产中典型的大延迟过程有传送物料能量、测量成分量、皮带运输、带钢连札机、以及多容量、多种设备串联等过程，都存在较大的时滞时间。延迟对系统品质具有较大影响，如使闭环特征方程中含有纯延迟因子、减低系统的稳定性等。

大迟延控制过程是较难控制的，为了改善大迟延系统的控制品质，

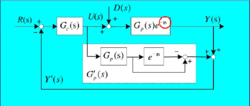
1957 年史密斯提出了一种以模型为基础的预估器补偿控制方法，即Smith 预估器。它的特点是预先估计出过程在基本扰动下的动态特性， 然后由预估器进行补偿，以减小超调量和加速调节过程。Smith预估器的原理图如图2所示。

Smith预估器是一种以模型为基础的预佑器补偿控制方法。其设计思想是预估出过程对扰动的动态响应，并将预估结果作为反馈提早供给控制器动作，以提前对扰动进行补偿。采用Smith预估补偿控制方法可以消除纯滞后环节对控制系统品质的影响。2