[科普中国]-扩展边界法

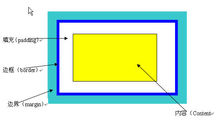
边界值定义

边界是指相对于输入等价类和输出等价类而言，稍高于其边界值及稍低于其边界值的一些特定情况。基于边界的方法是根据定义域来实现的，最终演变成边界值分析、健壮性测试、最坏情况测试和健壮最坏情况测试四种技术。

边界值分析也是一种黑盒测试方法，是对等价类分析方法的一种补充,由长期的测试工作经验得知，大量的错误是发生在输入或输出的边界上。因此针对各种边界情况设计测试用例，可以查出更多的错误。

关注边界值分析关注的是输入空间边界，用以标识测试用例，基本思想是在最小值（min）、略高于最小值（min+）、正常值（nom）、略低于最大值（max-）和最大值（max）等处取值。边界值分析手段主要有两种方式：通过变量数量和通过值域的种类进行。如一个n变量函数f（x1，x2，……xn）按以上方式每次确定一个测试对象（基于“单缺陷假设”理论），会产生4n+1个测试用例。健壮性测试是扩展边界值分析的测试，即增加一个略大于最大值（max+）和略小于最小值（min-）的取值，则用例数将变为6n+1。当边界值变量不是独立变量时，则以上测试用例就显的不充分。对于逻辑变量而言这种用例也没有什么用处。

最坏情况测试拒绝“单缺陷假设”理论的情况下，对所有变量的边界值集合进行5元素笛卡儿积计算，用以生成测试用例，对于n变量函数的最坏测试基于边界值分析会产生5n个测试用例，基于健壮性分析则产生7n个测试用例。相比而言最坏情况测试代价较高，因此其最佳运用是物理变量具有大量交互作用，或者函数失效的代价极高的情况下。

①“在最小值、和最大值处”是指的一般边界值分析。

②“略小于最小值、最小值、略高于最小值、正常值、略低于最大值、最大值、略大于最大值”其实是健壮性边界值分析，也就是考虑了非法的意外值。

③可靠性理论“单缺陷假设”：失效极少是由两个（或多个）缺陷的同时发生引起的。

原则一、如果输入条件规定了值的范围，则应该取刚达到这个范围的边界值，以及刚刚超过这个范围边界的值作为测试输入数据；

二、如果输入条件规定了值的个数，则用最大个数、最小个数、比最大个数多1格、比最小个数少1个的数做为测试数据；

三、根据规格说明的每一个输出条件，使用规则一；

四、根据规格说明的每一个输出条件，使用规则二；

五、如果程序的规格说明给出的输入域或输出域是有序集合（如有序表、顺序文件等），则应选取集合的第一个和最后一个元素作为测试用例；

六、如果程序用了一个内部结构，应该选取这个内部数据结构的边界值作为测试用例；

七、分析规格说明，找出其他可能的边界条件。

扩展边界条件法扩展边界条件法简称EBC法。最早是由P.C.Waterman提出来的，原用来求解导体的散射问题，后来推广应用到求解介质体，它的求解

步骤如下:

(1)采用等效原理，由外等效法以介质表面S上的电磁流替换介质体，此表面电磁流在S面外产生散射场，而在S面内产生与人射场大小相等方向相反的电磁场一Er与一r使S面的内场为零’。

(2)将采用等效原理得到的积分方程中的人射场和介质体内的场量均展开为矢量球面波函数。

(3)在S面上引用切向场连续的边界条件就可解得用人射场的展升系数表达的内场展开式中的待定系数。

(4)求出S面上内场的切向分量，由此解出散射场。

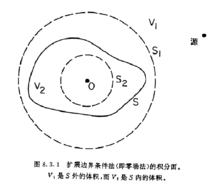
Waterman（1969，,1971）建立的扩展边界条件(EBC)法又称为零场法，它是求解面积分方程的方法之一。在该方法里，积分方程不直接加于表面S上，而是加于如图所示的S之外的表面S1和S2上以简化方程的求解。

标量场情况标量积分方程为

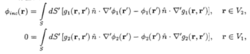
其中方程(1)适用于S包围的V2内的任何地方，而方程(2)适用于S外的V1任意地方。如果将积分方程(1)应用于V2内的一个球面S2上，将积分方程(2)应用于V1内的一个球面S1，则通常比较方便。这样做的另一优点是积分方程的解得到了简化。在这一方法里，积分方程施加于物体表面之外的一些表面上，故得名为扩展边界条件法(简称EBC法)。

如果用球谐函数展开场量，则在球面上的积分方程可以得到简化。例如，由加法定理，均匀介质的格林函数可展开。

但在实际应用中，通过舍去无限维数矩阵方程的高阶项，可以解出真与入射场幅度的关系。

在扩展边界条件法中，场仅仅在S2以内和S1以外被抵消。事实上，加在S1的表面源也会抵消S2以内任何一点或S以外任何一点的某些场。这样，扩展边界条件法所提供的解有时是实际解的近似，尽管在很多情形中，这种近似是非常好的。

由于检验表面S1和S2在扩展边界条件中总是处于表面S之外，所以如果S1和S2离开S的最大距离很大的话。矩阵方程将变得非常病态。例如，对于细长物体或呈波纹状的物体，便会出现上述问题。从物理上讲，对于这样的表面，在S上的表面源产生的场局部地集中于S的附近，使得问题变得病态(在平面波纹面的情况下，这种局部场其实是雕落波)。相应地，这些场在S上的信息在5：和S。上受到了大大削减，所以将积分方程施加于S1和S2上便得到了病态的方程。

Waterman的EBC法的收敛问题已由Bolomey和Wirgin(1974)及Bates和Wall(1977)研究过。尽管如此，由：尸它产生的方程较为简单，EBC法在很多应用问题里都是很有吸引力的。对于散射体周围的场可展开为球谐函数、柱谐函数，或伏洛盖(Floguet)模(如周期性粗糙表面)的情形，EBC法特别方便。

EBC法也很容易应用于不可贯穿物体。在此情况下，我们只需求解方程，其边界条件为齐次荻里赫莱或纽曼边界条件，或者是阻抗边界条件。由于完全不同的原因，由此推导的矩阵是病态的。这一内共振问题可以通过选择一个完备集来展开表面源而得到解决(见Waterman 1969)。1