[科普中国]-概率布尔网

定义

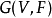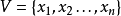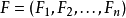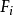概率布尔网络 中包含一个节点集合 和一个布尔函数集合序列 。集合 中的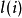 个布尔函数作为节点 的预测函数，

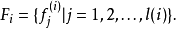
在每一步网络状态转移过程中，从集合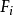 中以一定概率随机选择一个布尔函数作为节点 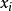的预测函数，所有被选取的预测函数构成了一个函数向量 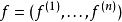，该函数向量称为 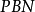的一个实现(realization)。 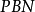的每个实现实际上都对应一个BN，因此可以看做是若干BN的概率组合。若每个节点预测函数的选择是相互独立的，则称该为独立的。独立的包含的BN的个数为

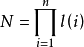其中BN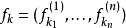 被选择的概率为

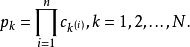
若对所有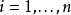 都与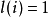 ，则BN的个数 ，此时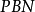 退化为BN。

概率布尔网络的动态特性可用马尔科夫链表述，其状态转移矩阵是一个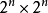 的矩阵，定义为

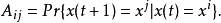考虑到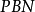 是有若干个BN组合成的，则

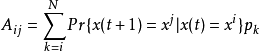其中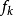 是被选中的函数。

例子假设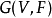 是一个包含三个节点的概率布尔网络，其中 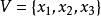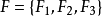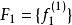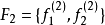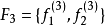， ， ， ， ，预测函数的真值表如表所示

|| ||

该概率布尔网络包含八个状态，其状态之间的转移关系如图所示

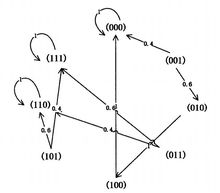
根据状态转移矩阵的定义可知，

与布尔网络模型的异同概率布尔网络与布尔网络的状态空间一致，大小均为2n；

布尔网络中任意状态都唯一确定一个后续状态，而概率布尔网络由于包含多个布尔网络，因此每个状态可能对应多个后续状态；

在布尔网络模型中，每个节点对应一个布尔函数，以该布尔函数作为其预测函数，布尔网络是一个决定性网络，网络当前状态完全且唯一决定网络的下一步状态。网络的状态沿初始状态在状态空间中形成一条轨迹。由于状态空间大小是有限的，这条轨迹最终将进入不动点或极限圈。而在概率布尔网络中，每个节点对应一个或多个预测函数，网络当前状态可能对应多个后续状态。

研究难点概率布尔网络研究中的一个重要问题是求其马尔科夫链相应的概率转移矩阵，并计算该矩阵的稳态分布。概率转移矩阵的稳态分布并不一定是存在的，为保证其稳态分布存在，可以在概率布尔网络中添加一个参数 。概率布尔网络中的节点状态以概率 受控于其预测函数集，而以概率 随机产生一个后续状态。这样，概率布尔网络的状态是强连通的，从而保证概率转移矩阵的稳态分布存在。

概率布尔网络的状态转移矩阵是一个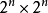的矩阵，当网络节点个数力很大时，求解其稳态分布很困难，因此如何简化概率布尔网络模型是一个有意义的问题2。目前概率布尔网络的一个简化方法是忽略其中的一些小概率的布尔网络3，其它的简化方法还有待探索。