[科普中国]-牵制控制

牵制控制的起源

在1990 年3位数学物理学家关于用小的反馈扰动控制混沌的开创性工作之后，混沌控制的研究取得了丰硕的成果。对于由大量混沌振子以某种规则拓扑耦合方式连接在一起而构成的时空混沌系统的控制也有不少的研究。其中研究较多的一种控制策略就是牵制控制。

牵制控制的原始基本思想是希望能够仅对网络中的一部分节点直接施加常数输入控制而达到有效抑制整个网络的时空混沌行为的目的。早期的工作包括由胡岗等人对由L个节点组成的一维离散时间最近邻祸合映像格子所做的探索，受控系统的状态方程为

其中 是相邻的两个被牵制控制节点之间的距离； 为被牵制节点的个数；当 时， ，否则 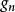； 是用来控制所牵制节点的反馈控制器。由于最初考虑的是常数输入，所以这种控制称为牵制控制。

牵制控制的理论研究Parekh等人针对离散时间耦合映像格子使用了牵制控制方法，研究发现，只有对网络中的每个节点都施加牵制控制，才能将耦合映像格子中的时空混沌稳定到平衡状态。 比较施加牵制控制的节点的不同分布，发现可以通过均匀或随机分布牵制控制节点来达到全局控制时空混沌的效果。因此，牵制控制的强度和控制器分布的密度都决定了耦合映像格子中时空混沌控制的有效性。Parekh 和Sinha 后来又进一步将耦合映像格子的时空混沌控制拓展到了反控制，即通过牵制控制，使得耦合映像格子由非混沌状态变为混沌状态，或者将耦合映像格子中比较弱的混沌进一步增强。牵制控制的思想同样被用于连续时间系统。

汪小帆和陈关荣最先考虑了如下一类连续时间线性耗散耦合动态网络模型的牵制控制

这里 为节点 的状态变量；常数 为网络的耦合强度；对角阵 表示两个耦合节点之间的具体的连接关系。耦合矩阵 为Laplacian矩阵。假设网络是连通的, 那么耦合矩阵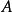 是一个对称且不可约矩阵，它有一个重数为1 的零特征根，而其余特征根均为负实数。

李翔、汪小帆和陈关荣接着考虑了如下更为一般的动态网络模型

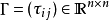其中 代表第 个节点和第 个节点直接按的耦合强度；矩阵 定义为如果存在一对 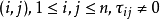，则两个相连的节点是通过它们各自的第 个分量和第 个分量耦合在一起。

可行性问题陈天平等人进一步的研究更为明确地指出仅对网络中的一个节点施加控制，就可以使得网络达到需要的同步状态。他们的工作是在内部耦合函数为单位矩阵时得到的。占萌等人研究最近邻网络中的牵制控制，在只对一个节点施加控制时，得到了在不同的内部祸合函数网络达到同步状态所需要的参数条件。卢文联将牵制控制策略开展到自适应动态网络中，除了对少量的节点增加控制器外，网络中的每个节点的状态的更新只依赖于节点的邻居状态。周进等人发现通过对少数节点施加控制使得具有一般拓扑的自适应网络牵制到同步状态。刘忠信和项林英等人将牵制控制策略推广到网络的祸合矩阵不能对角化的网络和具有时间延迟的加权网络中。Sorrentinal 等人定义网络牵制控制的可控性与节点之间的耦合强度、控制增益和进行牵制控制的节点数有关。

有效性问题上面介绍了牵制控制的可行性和稳定性分析。现在已经清楚，只要网络是连通的，那么就可以只对部分节点直接施加控制而使整个网络具有期望的同步状态。接下来的一个重要问题是有效性问题，即如何选取受控节点才能使得达到控制目标所花的代价尽可能小。这里的代价包括所需直接控制的节点数量、网络祸合强度和反馈控制增益幅值等。有效性问题与网络的拓扑性质密切相关。已有的研究表明，利用网络的拓扑特性，有选择地对网络中少量重要的关键节点直接施加控制要比随机选择部分节点加以控制具有明显优势。

无标度网络的特点是少数节点具有相对很高的度而大部分节点的度相对很低。牵制控制一般采用两种不同的牵制策略，一种是随机牵制，即在网络中随机地选择若干个节点施加牵制控制； 另一种是特定牵制， 即依次选择网络中度最大的若干节点施加牵制控制。无标度动态网络的特定控制的有效性可以从以下两个方面来理解：（1）在其它参数都相同的情况下，为达到控制目标，只控制那些度很大的节点所需要控制的节点个数，比随机牵制所需要控制的节点个数可能要少很多；（2） 如果选取数目相同的节点数加以控制, 那么为达到控制目标，特定牵制策略所需要的最小祸合强度可能比随机牵制策略所需要的最小耦合强度小很多。

以上介绍的是无向动态网络的牵制控制。对于有向动态网络的牵制控制的研究目前还不多。一种直观的想法是应该尽可能选取那些出度大的节点因为一个节点的出度越大，也就意味着该节点能够直接影响的邻居节点数目越多。但是，正如对于无向网络而言，度最大的节点未必一定是最重要的节点；对有向网络的牵制控制而言，出度最大的节点也未必是最重要的节点1。

动态特性分析在V稳定性架构下，牵制控制可认为是通过改变控制节点耗散度来实现控制目标。陈关荣等通过逻辑比较、层、收缩过程这三个概念对牵制控制网络的动态特性进行了分析。逻辑比较是建立在V稳定性的特征矩阵上，用来表明两个网络，即使具有不同的尺寸，哪个更容易被镇定。层是这样一个节点集合，其元素离控制节点具有相同距离。可以直观地认为，控制力是一层层的从控制节点传播至整个网络。收缩过程包含了节点收缩和边收缩两个过程具有收缩后网络比原先网络更难被镇定的特点。对于具有相同节点自动态和一致耦合强度的复杂网络，控制哪些使得第二层的输入连接度最大的节点是较好的选择。通过这些概念，可用一个层叠模型来估计被控制的复杂网络的V稳定性，其中节点表示网络的层，耦合强度为层的输入连接度。如果初始网络是V稳定的，那么对应的层叠模型也是V稳定的2。