[科普中国]-基于参数估计观测器

问题描述

对于给定动力系统

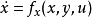
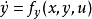x,y为系统状态，u为系统输入，其中y为可测部分，而x是需要估计状态，假设系统中所有映射足够光滑。对于该问题，状态观测器设计的目标是设计一个动力系统2

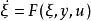
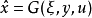
以保证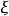有界，同时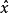渐近收敛到状态x。

PEBO的条件在对动力系统设计观测器时，系统需要同时满足三个性质，即可转化性、左逆性与可辨识性。

可转化性可转化性本质上是为一个偏微分方程可解性，即存在一个光滑映射h(y,u)使得如下的PDE需要存在解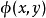

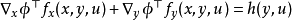
该偏微分方程在求解中，h(y,u)在自由项（free term），这就提高了PDE可解性，目前已经发现很多物理系统的动力学模型满足PEBO PDE。这样可以设计动态扩展（dynamic extension）

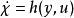
得到一个参数估计问题，要被估计的参数。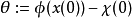

左逆性以上PDE解关于第一项要满足左可逆条件，即存在映射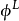满足

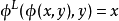
该条件条件很很多观测器中均存在，例如I&I观测器，KKL观测器等，该假设可以弱化为一定的单射条件。

可辨识性以上两个假设将状态重构转化为在线参数估计，余下的核心问题就是该参数（或向量）是否可以被估计出，这就要求系统满足一致可辨识性，即存在如下参数估计器

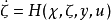
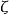使得有界，且

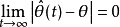
该假设在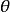具有线性结构的时候，可以类似于持续激励的条件。

PEBO设计结果若系统满足以上三个假设，可以按照上述观测器定义进行设计PEBO，其中映射选择如下：

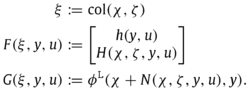
该PEBO可以所研究的系统的部分状态x进行渐近估计。

PEBO特点PEBO在非线性系统观测器设计中，主要的难点是PDE可解性，还要保证该解的可逆行。类似的观测器还有I&I观测器和Kazantzis–Kravaris–Luenberger观测器，但是它们所要求的PDE不同，因此所能应用的系统也不尽相同。

在PEBO中参数可辨识性要求不高，对于很多非线性参数回归，可以通过过参数化（over-parameterisation）的方法完成参数估计。

该方法本质上的缺陷是使用了纯积分环节，这样会对输出端的测量噪声相对敏感。但PEBO也已经证明在很多其他观测器无法解决的场合下，可以完成一些复杂的非线性系统的状态重构任务。

PEBO中的参数估计问题虽然是依赖于轨迹的，但是算法并不脆弱，这是因为参数估计是在线进行的。

系统的能观性并不意味着系统满足可转换性，可转换性也不意味系统满足能观性。

物理系统中的应用PEBO目前已经证明，在很多其他观测器无法应用的场景可以提供比较可靠的估计结果，例如无传感器控制下的磁悬浮系统，PMSM电机参数与磁通估计问题3，化工反应水槽液位估计，PLvCC机械系统，Cuk变压系统等。