[科普中国]-非线性双稳态系统

背景

随着人类认识能力的不断提高，己先后认识到了自然界的线性、非线性和复杂性，自然界从简单和谐变得越来越复杂，甚至变得模糊一片，这便是混沌.混沌是无序、无规律，这就是人们最早对混沌的认识.随着认识能力进一步提高，发现混沌原来也是有序的，而且可以控制和利用。事实上，自从在力学中首次注意到非线性，并在19世纪末，由Poincare用小参数法解决了三体问题开始，非线性力学就诞生了，而非线性科学也开始孕育了.随着各门分支学科非线性现象的不断发现和非线性学科的不断形成，上个世纪80年代，一门综合性的“非线性科学”诞生了。

自从1960年第一台激光器问世，人们就开始对光学非线性感兴趣，并在10多年后，发展成为一门新兴的“非线性光学”。线性光学成功地解决了介质的吸收、选择吸收、正常色散和反常色散等问题，其特点是同介质相互作用的外场比较弱，运动方程是线性的。由于激光的出现，人们已经有条件认识强场与介质相互作用，并先后发现了倍频、和频、差频和双稳态等与非线性有关的光学现象，并在电子学、光学和光电子学等科学和技术中找到重要应用。

注意到光学非线性是强光场与介质相互作用的结果，因此非线性光学不仅与外场有关，也与介质的结构和性质有关。最早，人们把具有中心对称的电介质(比如Ga, As等)填充到F-P干涉仪的两个反射镜之中，并从输出中反馈一个信号，得到了两个输出，系统出现了双稳态。人们利用藕合波理论成功地描述了这一现象。本文以不同的视角，直接从介质的非线性极化开始，在牛顿力学框架内，把偶极子的运动方程化为含有立方项的非线性微分方程，并用摄动法进行求解，找到了系统的频率响应曲线。结果表明，频率响应曲线出现了跳跃现象，正是这个跳跃现象决定了系统可能存在两个不同状态.事实上，当输入信号(外场振幅)取某些值时，系统的振幅可以取两个不同的值，而系统的两个不同振幅的平方正好对应着输出信号中两个不同的状态。

基本概念非线性系统：一个系统,如果其输出不与其输入成正比，则它是非线性的。从数学上看，非线性系统的特征是叠加原理不再成立。叠加原理是指描述系统的方程的两个解之和仍为其解。叠加原理可以通过两种方式失效。其一，方程本身是非线性的。其二,方程本身虽然是线性的,但边界是未知的或运动的。

双稳态电路：在电子电路中。其双稳态电路的特点是：在没有外来触发信号的作用下，电路始终处于原来的稳定状态。在外加输入触发信号作用下，双稳态电路从一个稳定状态翻转到另一个稳定状态。由于它具有两个稳定状态，故称为双稳态电路。双稳态电路在自动化控制中有着广泛的应用。

光学双稳态（optical bistability）是指光学系统具有多值性的现象。在一个非线性光学系统中，系统的输出光强和输入光强之间会出现类似于磁滞回线的滞后现象。光学双稳态是出现两个稳定透射状态的光学现象。光在二能级原子系统共振吸收时，如低入射光强，满足比尔定律。在输入光强 (I) 的某个范围内（c至d），对应每一输入光强I有两个可能输出光强(I0)a和b，它依赖于系统所处的历史状态。当输入光强从低值逐渐增加时，系统处在低态b，当输入光强从高值减小时，系统处在高态a。这种具有多值性的光学系统称为光学双稳态。

非线性双稳态系统：是指具有非线性系统的特点，同时具有双稳态系统的特点的系统。即指输入和输出不成正比，同时在没有外来触发信号的作用下，电路始终处于原来的稳定状态。在外加输入触发信号作用下，双稳态电路从一个稳定状态翻转到另一个稳定状态的系统。

条件光学系统具有双稳态的条件：系统必须是非线性的；系统中要有反馈机制。一个常见例子是含有非线性介质的法布里－珀罗腔。

原理光在二能级原子系统共振吸收时，如低入射光强，满足比尔定律，透射光强与入射光强成正比；但如入射光强很高，就出现吸收的非线性－饱和吸收，明显地偏离比尔定律。此时，介质变得几乎透明，因而透射光强几乎与入射光强一样大。入射光强与透射光强之间的这种关系，可用一个单值函数来表示。如果把这种二能级原子系统的吸收介质放在法布里－珀罗腔内，由于吸收过程的非线性和腔的反馈过程的相互作用，当入射光强逐渐增加时，透射光强缓慢地单调上升；当入射光强到达某一临界值时，系统突然透明，透射光强几乎与入射光强相等；如果这时减小入射光强，则系统会保留在高透射状态，不经原路线回到低透射状态；直到入射光强到达另一临界值时，系统才回到低透射状态，此时介质又重新变成强吸收体。这种入射光强与透射光强间具有滞后回线的特性，造成在一定区间内的每一入射光强对应透射光强有两个稳定的状态：高透射状态和低透射状态，这种现象称为光学双稳态。系统究竟处于何种透射状态不仅与入射光强有关，还与过去所处状态有关。1

光学非线性双稳态概念最早（1969）是在可饱和吸收介质的系统中提出的，并于1976年首次在钠蒸气介质中观察到。随入射光强而变化的非线性介质，也观察到光学双稳态。并且有比吸收介质更为优越的性能，比如，观察到光学双稳态的入射光强更低，对光源的线宽没有更高要求，也没有吸收引起的热耗散问题，因而在光学双稳态的应用上比吸收型装置更为受人重视。

光学双稳态除在非线性法布里－珀罗腔内观察到外，还在诸如光电反馈混合装置、非线性界面、声光装置、自聚焦等实验中被观察到。

非线性系统分类非本质非线性:能够用小偏差线性化方法进行线性化处理的非线性。2

本质非线性:用小偏差线性化方法不能解决的非线性。

意义“线性”与“非线性”是两个数学名词。所谓“线性”是指两个量之间所存在的正比关系。若在直角坐标系上画出来，则是一条直线。由线性函数关系描述的系统叫线性系统。在线性系统中，部分之和等于整体。描述线性系统的方程遵从叠加原理，即方程的不同解加起来仍然是原方程的解。这是线性系统最本质的特征之一。“非线性”是指两个量之间的关系不是“直线”关系，在直角坐标系中呈一条曲线。最简单的非线性函数是一元二次方程即抛物线方程。简单地说，一切不是一次的函数关系，如一切高于一次方的多项式函数关系，都是非线性的。由非线性函数关系描述的系统称为非线性系统。

区别定性地说，线性关系只有一种，而非线性关系则千变万化，不胜枚举。线性是非线性的特例，它是简单的比例关系，各部分的贡献是相互独立的；而非线性是对这种简单关系的偏离，各部分之间彼此影响，发生耦合作用，这是产生非线性问题的复杂性和多样性的根本原因。正因为如此，非线性系统中各种因素的独立性就丧失了：整体不等于部分之和，叠加原理失效，非线性方程的两个解之和不再是原方程的解。因此，对于非线性问题只能具体问题具体分析。

线性与非线性现象的区别一般还有以下特征：

（1）在运动形式上，线性现象一般表现为时空中的平滑运动，并可用性能良好的函数关系表示，而非线性现象则表现为从规则运动向不规则运动的转化和跃变；

（2）线性系统对外界影响的响应平缓、光滑，而非线性系统中参数的极微小变动，在一些关节点上，可以引起系统运动形式的定性改变。在自然界和人类社会中大量存在的相互作用都是非线性的，线性作用只不过是非线性作用在一定条件下的近似。

非线性双稳态电路由两个或非门组成，有两个输入端和两个输出端

图 1 是用分立元件构成双稳态电路的基本形式，图 2 是电路中各点电压波形。

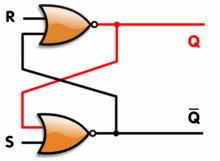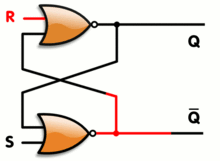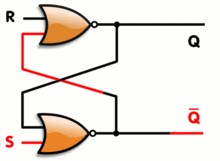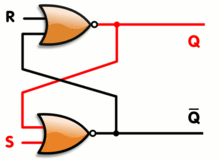
晶体管 PNP 型 V1 、 V2 是二个反相器。交叉耦合构成双稳态电路，每个反相器的输出端通过电阻分别耦合到另一个反相器的输入端。由于反相器的输入和输出信号是反相的，很容易形成二个稳定状态： V1 截止 V2 导通。这是一个稳定状态；反之， V1 导通， V2 截止，这又是一个稳定状态； Rc1 、 Rc2 是 V1 、 V2 的负载电阻， Rk1 、 Rk2 是二个晶体管级间耦合电阻。为了保证晶体管快速截止，用 RB1 、 RB2 及电源 EB 为各个晶体管的基极提供反偏置。两管集电极的 A 点和 B 点是两个输出端，这种电路一般是对称的，即 Rc1=Rc2,RB2=RB2 ，两管参数亦应相同。

意义和发展光学非线性双稳态已进行了广泛研究，包括各种激光系统，诸如半导体激光器、塞曼激光器、有饱和吸收体激光器、参量振荡器、染料激光器等的研制；非线性界面上反射和含非线性介质（如Na蒸气）法布里－珀罗腔或双向环形腔等被动光学系统探讨；光电混合装置的制作等。光学双稳态因在协同学和耗散结构中作为远离平衡态的开放系统的一个典型例子而具理论意义1。系统的外界参量改变时，可观察到自脉冲和混沌现象，成为研究分岔和混沌的有力实验装置。由于观察到“光学浑沌”（在一完全确定的非线性系统中，当改变参量时，出现类似随机的行为，称为浑沌）而受到理论物理界的重视，为研究非平衡统计物理提供了一种重要实验手段。此外，光学双稳态可制成光学限幅器、光开关等器件，在光计算中得到应用。

光学非线性双稳态引起人们极大注意的主要原因是光学双稳器件应用在高速光通信、光学图像处理、光存储、光学限幅器以及光学逻辑元件等方面。尤其是用半导体材料（GaAs，InSb等）制成的光学双稳器件，尺寸小（几毫米直径，几十至几百微米厚），功率低（10微瓦/微米2—1毫瓦/微米2），开关时间短（约10－12秒），成为未来光计算机的逻辑元件。