[科普中国]-复合离散混沌系统

基本概念

混沌现象是在非线性动力系统中表现的确定性、类随机的过程，这种过程既非周期又不收敛，并且对于初始值具有敏感的依赖性。

按照动力学系统的性质，混沌可以分成四种类型：

1）时间混沌；

2）空间混沌；

3）时空混沌；

4）功能混沌；

复合离散混沌系统是一类特殊的混沌系统，它由两个(或多个)离散混沌系统通过一定的规则构成与离散混沌系统相比，复合离散混沌系统的迭代过程不仅具有对初始条件的敏感性，而且具有依照双序列选择迭代函数的灵活性，因此迭代过程还具有一定的随机性。

数学描述设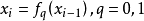 是两个离散混沌动力系统，对任意序列 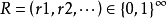，则

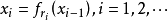
为这两个迭代系统在序列R下的复合离散混沌动力系统，记为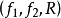 ，其中R称为复合序列。对q=0或q=1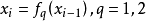， 称为它的子系统。

复合迭代系统式的动力行为与复合序列R有关，若当i充分大时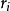， 为常数，则复合迭代系统退化为单一混沌系统一般地，复合迭代系统保持了所有子迭代系统的混沌特性，其行为也要比单个子迭代系统复杂得多1。

离散混沌系统一维离散混沌系统一个一维离散时间非线性动力学系统定义如下：

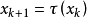
其中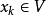，，我们称之为状态。 而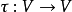是一个映射，将当前状态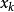映射到下一个状态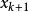。如果我们从一个初始值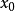开始，反复应用， 就得到一个序列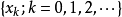。这一序列称为该离散时间动力系统的一条轨迹。

一类非常简单却被广泛研究的动力系统是logistic映射，它起源于虫口模型。

二维离散混沌系统一维离散混沌系统，具有形式简单、产生混沌序列时间短等优点，但其缺点是密钥空间太小。用二维超混沌系统生成的混沌序列，变换成加密因子序列。

Lyapunov指数（简称李氏指数），是刻画非线性系统混沌特性的有效方法之一，李氏指数的个数与系统状态空间的维数n相同。如果只有一个李氏指数大于零，则系统是混沌的；若至少有两个李氏指数大于零，则系统是超混沌的。大于零的李氏指数越多，系统不稳定的程度越高。一般来说，系统的状态量个数越多（如高维系统，对离散系统来说，n>2），它可能出现不稳定的程度越高2。

不失一般性，二维混沌离散系统有如下形式：

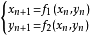采用高维系统产生超混沌，由于系统比低维情况复杂，产生超混沌时序的时间增长，将有可能直接影响保密通讯实时性的要求。因此，如何在系统状态变量个数尽可能少而正性李氏指数又尽可能多的条件下，寻找到非线性形式简单的系统，是十分实际而又有意义的工作。为了寻找简单形式饿二维离散超混沌系统，需要进一步简化，使部分非线性项前面的系数为零，然后通过计算该系统的李氏指数，即有两个或两个以上大于零的李氏指数，可认为该系统是超混沌特性的二维离散系统。

应用混沌应用可分为混沌综合和混沌分析。前者利用人工产生的混沌从混沌动力学系统中获得可能的功能，如人工神经网络的联想记忆等；后者分析由复杂的人工和自然系统中获得的混沌信号并寻找隐藏的确定性规则，如时间序列数据的非线性确定性预测等。

混沌的具体的潜在应用可概括如下：

（1）优化：利用混沌运动的随机性、遍历性和规律性寻找最优点，可用于系统辨识、最优参数设计等众多方面。

（2）神经网络：将混沌与神经网络相融合，使神经网络由最初的混沌状态逐渐退化到一般的神经网络，利用中间过程混沌状态的动力学特性使神经网络逃离局部极小点，从而保证全局最优，可用于联想记忆、机器人的路径规划等。

（3）图像数据压缩：把复杂的图像数据用一组能产生混沌吸引子的简单动力学方程代替，这样只需记忆存储这一组动力学方程组的参数，其数据量比原始图像数据大大减少，从而实现了图像数据压缩。

（4）高速检索：利用混沌的遍历性可以进行检索，即在改变初值的同时，将要检索的数据和刚进入混沌状态的值相比较，检索出接近于待检索数据的状态。这种方法比随机检索或遗传算法具有更高的检索速度。

（5）非线性时间序列的预测：任何一个时间序列都可以看成是一个由非线性机制确定的输入输出系统，如果不规则的运动现象是一种混沌现象，则通过利用混沌现象的决策论非线性技术就能高精度地进行短期预测。

（6）模式识别：利用混沌轨迹对初始条件的敏感性，有可能使系统识别出只有微小区别的不同模式。

（7）故障诊断：根据由时间序列再构成的吸引子的集合特征和采样时间序列数据相比较，可以进行故障诊断3。