[科普中国]-非线性时变系统

非线性系统简介

非线性系统是指一个系统,如果其输出不与其输入成正比，则它是非线性的。从数学上看，非线性系统的特征是叠加原理不再成立。叠加原理是指描述系统的方程的两个解之和仍为其解。叠加原理可以通过两种方式失效。其一，方程本身是非线性的。其二,方程本身虽然是线性的,但边界是未知的或运动的。

分类非本质非线性：能够用小偏差线性化方法进行线性化处理的非线性。

本质非线性：用小偏差线性化方法不能解决的非线性。

线性与非线性的意义与区别意义

“线性”与“非线性”是两个数学名词。所谓“线性”是指两个量之间所存在的正比关系。若在直角坐标系上画出来，则是一条直线。由线性函数关系描述的系统叫线性系统。在线性系统中，部分之和等于整体。描述线性系统的方程遵从叠加原理，即方程的不同解加起来仍然是原方程的解。这是线性系统最本质的特征之一。“非线性”是指两个量之间的关系不是“直线”关系，在直角坐标系中呈一条曲线。最简单的非线性函数是一元二次方程即抛物线方程。简单地说，一切不是一次的函数关系，如一切高于一次方的多项式函数关系，都是非线性的。由非线性函数关系描述的系统称为非线性系统。

区别

定性地说，线性关系只有一种，而非线性关系则千变万化，不胜枚举。线性是非线性的特例，它是简单的比例关系，各部分的贡献是相互独立的；而非线性是对这种简单关系的偏离，各部分之间彼此影响，发生耦合作用，这是产生非线性问题的复杂性和多样性的根本原因。正因为如此，非线性系统中各种因素的独立性就丧失了：整体不等于部分之和，叠加原理失效，非线性方程的两个解之和不再是原方程的解。因此，对于非线性问题只能具体问题具体分析。

线性与非线性现象的区别一般还有以下特征：

（1）在运动形式上，线性现象一般表现为时空中的平滑运动，并可用性能良好的函数关系表示，而非线性现象则表现为从规则运动向不规则运动的转化和跃变；

（2）线性系统对外界影响的响应平缓、光滑，而非线性系统中参数的极微小变动，在一些关节点上，可以引起系统运动形式的定性改变。在自然界和人类社会中大量存在的相互作用都是非线性的，线性作用只不过是非线性作用在一定条件下的近似。

时变系统简介时变系统(time-varying system)其中一或一个以上的参数值随时间而变化，从而整个特性也随时间而变化的系统。时变系统的特点是，其输出响应的波形不仅同输入波形有关，而且也同输入信号加入的时刻有关。

特点时变系统的特点是，其输出响应的波形不仅同输入波形有关，而且也同输入信号加入的时刻有关。这一特点增加了分析和研究的复杂性。对于时变系统来说，即使系统是线性的,也只能采用时间域的描述。描述的基本形式是变系数的微分方程或差分方程。时变系统的运动分析比定常系统要复杂得多。在工程中，应用最广的是所谓冻结系数法，这一方法的实质是在系统工作时间内，分段将时变参数“冻结”为常值，从而可分段地把系统看成为定常系统进行研究。通常，冻结参数法只对参数变化比较缓慢的时变系统才有效。对时变系统控制的一个可能的方案是，在采用估计器对参数进行在线估计的同时，采用适应控制系统实现控制。

分析在工程中，应用最广的是所谓冻结系数法，这一方法的实质是在系统工作时间内，分段将时变参数“冻结”为常值，从而可分段地把系统看成为定常系统进行研究。通常，冻结参数法只对参数变化比较缓慢的时变系统才有效。对时变系统控制的一个可能的方案是，在采用估计器对参数进行在线估计的同时，采用适应控制系统实现控制。

非线性时变系统特点非线性时变系统即同时满足非线性系统和时变系统特征的系统，它满足系统其输出不与其输入成正比的特点，同时，当系统中某个参数值随时间而变化时，整个特性也随时间而变化。

稳定性分析复杂在无外作用且系统输出的各阶倒数等于零时.系统处于平衡状态。显然，对于线性系统只有一个平衡状态；而对于非线性系统，则可能存在多个平衡状态，有稳定的平衡状态和不稳定的平衡状态，需要具体分析。

可能存在自激振荡自激振荡是指没有外界周期变换信号的作用时，系统内产生的具有固定振幅和频率的稳定周期运动简称自振.

线性系统不可能形成稳定的自激振荡，而非线性系统在满足一定条件下可能形成稳定的自振。

频率响应发生畸变非线性时变系统分析方法描述函数法在正弦输入信号作用下，非线性时变系统的稳态输出中一次谐波分量和输人信号的复数比为非线性环节的描述函数，用N(A)表示，即1

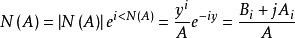
逆系统法逆系统

所谓系统相当于对象在给定初始条件下。输入到输出的一个变换，即

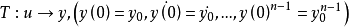
n为系统阶次。y为n阶可微函数。

若在满足初始条件的情况下，存在一个系统即变化，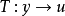

则称该系统为原系统的逆系统。即有:

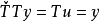
伪线性系统

将n阶积分逆系统和原系统相串联成复合系统，称为伪线性系统。

线性控制的逆系统没计方法

①状态反馈控制。

②渐进跟踪控制。