[科普中国]-纯整数线性规划

整数规划问题的数学模型

要求一部分或全部决策变量必须取整数值的规划问题称为整数规划(integer programming，简记IP)。不考虑整数条件，由余下的目标函数和约束条件构成的规划问题称为该整数规划问题的松驰问题( slack problem )。若松驰问题是一个线性规划，则称该整数规划为整数线性规划(integer linearprogramming)。

整数线性规划数学模型的一般形式为：

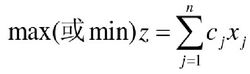
分类整数线性规划问题可以分为下列几种类型：

（1）纯整数线性规划(Pure integer linear programming)：指全部决策变量都必须取整数值的整数线性规划。有时，也称为全整数规划。

（2）混合整数线性规划(Mimed integer linear programming)：指决策变量中有一部分必须取整数值，另一部分可以不取整数值的整数线性规划。

（3）0-1型整数线性规划((Zero-one integer linear programming)：指决策变量只能了取值0或1的整数线性规划。

整数规划解的特点松驰问题作为一个线性规划问题，其可行解的集合是一个凸集，任意两个可行解的凸组合仍为可行解。整数规划问题的可行解是它松驰问题可行解集合的一个子集，任意两个可行解的凸组合不一定满足整数约束条件，因而不一定仍为可行解。由于整数规划问题的可行解一定也是它的松驰问题的可行解(反之则不一定)，所以，前者最优解的目标函数值不会优于后者最优解的目标函数值，即松弛问题的最优解是整数规划问题最优解的上限。

在一般情况下，松驰问题的最优解不会刚好满足变量的整数约束条件，因而不是整数规划的可行解，自然就不是整数规划的最优解。此时，若对松驰问题的这个最优解中不符合整数要求的分量简单地取整，所得到的解不一定是整数规划问题的最优解，甚至也不一定是整数规划问题的可行解。

求整数规划的方法典型的求整数规划的方法有割平面法、分支定界法、完全枚举法、以及适用于指派问题的匈牙利解法等。

（1）完全枚举法：对于可行域有界的整数线性规划问题，整 数线性规划的可行解是一个有限集，将 这个集内的每一个点对应的目标函数值 都一一计算出来，然后从中找出最优者 ，则为整数线性规划的最优解。适于变量个数不大于10的0-1型整数线性规划。

（2）分支定界法：分支定界解法是一种部分枚举法，通过不断地 分割松弛问题的可行域并进行比较，最终求得整数线性规划问题的最优解。它的解题思路是先求解整数线性规划的松弛问题，如果其最优解不符合整数条件，则用增加约束的办法求出整数线性规划问题的上下界，并把松弛问题的可行域分成互不重叠的子区域，再求解这些子区域的松弛问题，不断缩小整数线性规划问题上下界的差距，最后取得整数线性规划问题的最优解。

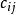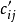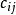（3）匈牙利解法的思路为：1）若从指派问题的系数矩阵（）的某行(或某列)各元素分别减去一个常数k，得到一个新的矩阵（），为（）和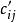（）为系数矩阵的两个指派问题有相同的最优解。2）独立0元素：位于不同行不同列的0元素。3）若在系数矩阵中找到n个独立0元素，则对应的指派方案总费用(或时间、成本等) 为零，即为原指派问题的最优解。

（4）割平面法：割平面法是R. E. Gomory于1958年提出的一种方法，它主要用于求解纯整数规划。若伴随规划的最优解不满足整数约束，则有两条途径可走：

1）将整数规划问题分解成几个子规划，只要不断查清子问题的解的情况，原问题也因此得到解决。(即分枝定界法)

2）不断切割原问题伴随规划的可行域，使它在不断缩小的过程 中，将原问题的整数最优解逐渐暴露，且趋于可行域极点的位置。(即割平面法)1