[科普中国]-自适应逻辑系统

基本概念

自适应逻辑系统(adaptive logic system，简称ALS)并不是通常意义上的逻辑系统，而是一个形式化的证明框架。自适应逻辑的主要特点是它能够灵活地适应具体的前提集合，根据特定的异常标准“尽可能正常地”解释前提集合，为被解释的推理过程界定一种后承关系。其动态证明使其成为刻画可废止推理的一个有效工具。

“自适应”一般是指系统按照环境的变化，调整其自身使得其行为在新的或者已经改变了的环境下达到最好的或者至少是容许的特性和功能，这种对环境变化具有自适应能力的系统称为自适应系统。在反馈控制和最优控制中，都假定被控对象或过程的数学模型是已知的，并且具有线性定常的特性。实际上在许多工程中，被控对象或过程的数学模型事先是难以确定的，即使在某一条件下被确定了的数学模型，在工况和条件改变了以后，其动态参数乃至于模型的结构仍然经常发生变化。在发生这些问题时，常规控制器不可能得到很好的控制品质。为此，需要设计一种特殊的控制系统，它能够自动地补偿在模型阶次、参数和输入信号方面非预知的变化，这就是自适应控制。

自适应逻辑系统的分类自从50年代末期由美国麻省理工学院提出第一个自适应控制系统以来，先后出现过许多不同形式的自适应控制系统。主要有：

（1）增益自适应控制

（2）模型参考自适应控制（MRAC）

（3）自校正控制（STC）

（4）直接优化目标函数自适应控制

（5）模糊自适应控制

（6）多模型自适应控制

（7）自适应逆控制

模型参考自适应控制（model reference adaptive system，MRAS）和自校正控制系统（self-tuning control system）是目前比较成熟的两类自适应控制系统。这类自适应系统的一个主要特点是在线辨识对象数学模型的参数，进而修改控制器的参数1。

模型参考自适应控制系统这类自适应控制系统设计方法的理论基础为局部参数优化方法、李雅普诺夫稳定性理论和波波夫（Popov）超稳定性理论。

模型参考白适应控制系统由参考模型、被控对象、反馈控制器和调整控制器参数的自适应机构等部分组成，其基本原理如图1所示。这类控制系统包括内回路和外回路两个回路。内环是由被控对象和控制器组成的普通反馈回路，而控制器的参数则由外回路调整。参考模型的输出 直接表示了对象输出应当怎样理想地响应参考输入信号r。

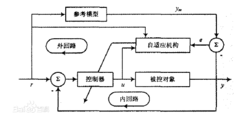图1

控制器参数的自适应调整过程如下：

当参考输入r(t)同时加到系统和模型的入口时，由于对象的初始参数未知，控制器的初始参数不可能整定得很好。故一开始，运行系统的输出响应y(t)与模型的输出响应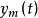 是不可能完全一致，结果将产生偏差信号e(t)，故可由e(t)驱动自适应机构来产生适当调节作用，直接改变控制器的参数，从而使系统的输出 y(t)逐步与模型输出 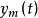接近，直到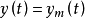 为止，当e(t)=0后，自适应调整过程就自动停止，控制器参数也就自动整定完毕。

自校正控制系统(STC)自校正控制系统可以设想由两个环路组成，其典型结构如图2所示。

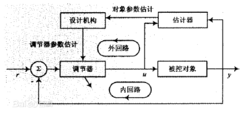图2

该调节器的内环包括被控对象和一个普通的线性反馈调节器，外环则由一个递推参数估计器和一个设计机构所组成，其任务是辨识过程参数，再按选定的设计方法综合出控制器参数，用以修改内环的控制器。这类系统的特点是必须对过程或者被控对象进行在线辨识（估计器），然后用对象参数估计值和事先规定的性能指标在线综合出调节器的控制参数，并根据此控制参数产生的控制作用对被控对象进行控制。经过多次地辨识和综合调节参数，可以使系统的性能指标趋于最优。

在目前的自校正控制系统中，用来综合自校正控制律的性能指标有两类：优化性能指标和常规性能指标。前者如最小方差、LQG和广义预测控制；后者如极点配置和PID控制；用来进行参数估计的方法有最小二乘法、增广矩阵法、辅助变量法和最大似然法。

自适应逻辑控制的应用模型参考自适应控制系统的应用MRAC系统过去应用最成功的领域之一是电力拖动领域。例如，最早应用的是Courtial和Landau对晶闸管供电直流电力拖动系统进行的自适应控制。南于使用常规的PI调节器进行速度反馈控制不能保证要求的高性能指标，而采用自适应控制方案可将对象近似为二阶系统，且只调两个参数就能保证对象参数变化时性能指标不变，并能克服电机速度过零时，PI调节器不能解决的死区问题。

MRAC技术在自动机上应用也很活跃，可基本上解决自动机的非线性和自由度间的干扰问题。MRAC技术在船舶自动驾驶方面应用也很成功，它可将非线性模型简化为二阶线性模型，这样，当外界环境（风力，波浪，水流等）变化，使船的动力特性随吃水差、负载和水深而改变时，采用自适应控制的自动驾驶仪就可达到要求的性能，操作安全可靠。另外，MRAC技术在其他领域也有应用，诸如内燃机，吹氧炼钢炉，液压伺服系统等。

自校正控制系统的应用目前自校正控制系统应用要比MRAC多得多，除造纸、化工、二氧化钛窑、水泥工业、矿石粉碎、单晶炉圆筒锅炉等外，在超级游轮自动驾驶和船舶自动驾驶克服随机干扰，如风、浪、潮流、速度、负载及水深等方面效果也很好。同时，在原子能工业、机器人和人工心脏等部门中的应用也不乏成功的例子。

自适应逻辑系统存在的问题稳定性问题稳定性问题是一切控制系统的核心问题。设计自适应控制系统应以保证系统全局稳定为原则。现已发现现有的稳定性理论还不能处理已提出的一些自适应控制问题，尚需建立一种新的稳定性理论体系M。

收敛性问题当一个自适应控制算法被证明是收敛时，它可以提高这个算法在实际应用中的可信度。由于自适应算法的非线性特性对建立收敛理论带来较大的困难，目前只在有限的几类简单的自适应控制算法中取得了一定的结果。而且现有的收敛性结果的局限性太大，假设条件限制太严，不便于实际应用，即便是保证参数估计收敛的最基本要求，对于实际系统也不一定总能满足。收敛性的理论研究还有待进一步深入。

鲁棒性问题在存在扰动和未建模动态特性的条件下，系统能保证其稳定性和一定动态性能的能力称之为自适应控制系统的鲁棒性。扰动能使系统参数产生严重漂移，导致系统的不稳定，特别是在存在未建模的高频动态特性的条件下，若指令信号过大或含有高频成分，或存在高频噪声，或自适应增益过大，都可能使自适应控制系统丧失稳定性。目前，已提出若干不同方案来克服上述原因导致的不稳定，但还远不能令人满意。今后一个重要的理论研究课题就是要设计一个鲁棒性强的自适应控制系统。

性能和稳定性问题一个自适应控制系统的很好工作，不仅要求所设计的系统稳定，而且要满足一定的性能指标要求。由于自适应控制系统是非线性时变系统，初始条件的变化或未建模，其动态存在都势必要改变系统的运动轨迹。因此，分析自适应控制系统的动态品质是极其困难的。目前，这方面成果还很少见2。