[科普中国]-非线性自适应逆控制

自适应逆控制(AdaptivelnverseControl)是由美国斯坦福大学著名教授B．Widrow于1986年首次命名并提出来的，当时在学术界引起了很大反响，为设计控制系统和调节器开辟了新途径。它是用自适应滤波方法辨识出被控对象的逆模型，串联到对象的输入端作为控制器来控制对象的动态特性，所以称为自适应逆控制。自适应逆控制中的反馈是属于局部反馈，在自适应迭代过程中只用于改变模型参数，并不直接控制主回路中的信号流动，更没有输出到输入的闭环，所以它是开环控制。自适应逆控制系统中的动态特性控制和消除扰动控制是分开来各自独立完成的，互不影响，所以可尽最大可能提高各自的性能。所以自适应逆控制与传统反馈控制和自适应控制在原理上截然不同。1

从自适应逆控制的基本理论和方法来看：自适应逆控制涉及到自适应数字信号处理和控制两个学科(交叉)，也就是用自适应数字信号处理的方法来研究未知系统自适应逆控制问题。

从所需要的数学基础来看：自适应逆控制主要涉及概率、数理统计和矩阵代数等知识：而自适应控制还需要除此之外的一些高深数学，使广大控制工程师们难以掌握，更难以应用。

从适用范围来看：对象是稳定的和不稳定的；最小相位的和非最小相位的：线性的和非线性的，单输人单输出和多输人多输出等系统的控制问题。并能解决自适应控制所不能解决的问题。

自适应逆控制和自适应滤波的简单比较：

在已经过去的20年中，各种期刊和会议论文集已发表了大量自适应控制方面的论文，与此同时，也刊出了很多自适应信号处理方面的论文，并出版了不少专著。这两种学派几乎是各自独立发展着。大体上来说：控制理论工作者在研究自适应控制时，是用状态变量进行反馈，通过设计出来的自适应律来调节参数(或称为权系数)，达到控制对象的性能和抑制扰动的目的。非线性自适应逆控制及其应用(或称为权系数)进行适时调整(或称为自适应调整)，用这样的方法得到的线性或非线性自适应滤波器用到线性或非线性信号处理系统中去，它们各自找到了应用的场合。

自适应逆控制已作为一种新的控制方法应用于复杂、未知和不确定的非线性动态系统控制中。它用被控对象逆的传递函数作为控制器，这个控制器能够自适应的调节自身参数使得对象的动态响应达到最优。当然，要实现这一目的主要依靠逆模型，可是在实际应用中，对于一个复杂的、未知的和不确定的非线性对象模型，怎样设计其精确的逆模型，仍是逆控制应用于实际的障碍。

自适应逆控制原理在很多文献中已经得到应用，但是对于非线性对象的控制仍不够完善。本书将自适应逆控制应用于非线性单输入单输出(SISO，Singlel：真putSingleOutput)对象控制，此外，有些方法也可推广到非线性多输人多输出(MIMO，MultiplylnputMultiplyOutput)对象中去用更复杂的系统来控制。严格的来说，自适应逆控制方法能否应用，取决于非线性系统的逆的存在性和准确性，这将在后面说明。在这种情况下，非线性对象的逆控制能够做到，而且通过采用非线性滤波也能做到对非线性对象的扰动进行控制。

综上所述，非线性自适应逆控制的成立主要基于两个方面:

(1)非线性模型和算法能够对任意的非线性模型有逼近能力，即能够对任意的非线性系统进行精确的建模。

(2)非线性系统的逆模型的存在性和精确性。

不同于前面给出的传统反恢控制和自适应控制方式，从某种意义上说是一个开环控制，而前者是闭环控制。它是借助于自适应德波方面的知识建立起来的控制方式—自适应逆控制，这种控制方式便于理解和应用。

如图所示为自适应逆控制的方框图：用非线性对象传递函数的逆作为控制器去驭动对象，因为对象是未知的，这就要先辨识出对象的逆，并用某一种自适应算法调节控制器参数使得对象输出与指令输人误差方差最小。这样非线性对象输出就跟随上指令输人。从图可看出，只有控制器是对象传递函数的逆时，上臂传递函数才是1，与指令输人之差最小，在理想情况下是0。

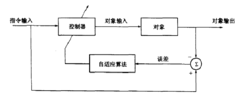
上述结果是假定对象为非线性的、参数是慢时变的(在调整过程中认为参数不变可按定常处理)，这可看成是准静态平稳时才成立，与MRACS的假定是相同的。

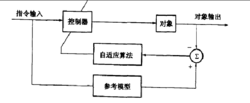
有时要求对象跟踪的不是指令愉人而是参考模型愉出，如图所示，这时称为模型参考自适应逆控制系统。参考模型的动态响应应选择与对象期望的动态响应一致。当误差趋向于0时，对象便跟随上参考模型，模型的性能指标便是对象的性能指标。这里用的性能指标是模型和对象动态响应误差方差最小。这时上臂控制器与对象串联的传递函数近似等于参考模型的传递函数，在理想情况下二者相等。

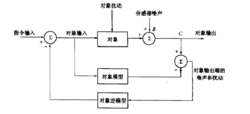
如图所示，对象输出存在着扰动和测量噪声。为使对象输出或动态响应中不存在噪声和扰动，提高对象输出的动态品质，就要想办法将其去掉。怎样去掉呢?图中给出了消除办法：将辨识出的对象模型与对象并联，在同一个对象输人作用下比较其输出，则两者的偏差就近似等于对象扰动和测量噪声之和，在辨识模型是理想的情况下，二者之差便完全等于对象扰动和测量噪声之和。

要想实现非线性自适应逆控制，起决定性作用的是非线性系统建模的精确性和稳定性。随着神经网络、模糊控制和神经网络模糊控制等非线性算法的日趋完善。

我们能够构造良好的非线性自适应逆控制系统。实际上，神经网络、连续函数、神经网络、模糊控制器和离散模糊专家系统之间存在数值等效关系，它们都可以逼近连续函数，且它们之间又都可以相互通近，可以构造既在计算上完全等效于模彻系统又具有神经网络结构和学习机制的混合神经网络。

逆系统控制的基本思想是求解对象逆系统方程，然后用它进行补偿，使复合系统在大范围内成为线性或接近线性的系统。从而可采用线性系统的控制器综合方法，设计出实用的大范围稳定的控制器。一些学者在时域内讨论了逆系统的控制器综合方法。但所提出的方法都要求系统有比较精确的模型描述。广义频域响应的基础上，构造一个非线性补偿器，使补偿器与对象构成的复合系统高于一阶的GFRF为0。但实际上由于大部分非线性系统具有无限阶Volerra核，不可能完全补偿，而只能使前若干阶Volerra核补偿为0，使复合系统近似于线性系统。对于复合系统的控制。可以用常规的自适应控制方法进行。

这种综合方法的一般步骤:

(1)计算补偿器G的GFRF模型;

(2)获得G的GFRF模型的微分方程实现;

(3)对补偿后的近似线性系统，利用各种传统控制方法设计线性控制器。