简介
线性二次控制(Linear quadratic control)是指线性的,性能指标泛函是状态变量和控制变量的二次型函数的积分,并且由状态变量构成线性状态反馈方式。
如果系统是线性的,性能指标泛函是状态变量和控制变量的二次型函数的积分,并且由状态变量构成线性状态反馈系统,则这样的最优控制称为线性二次最优控制。以下介绍的是线性二次型最优控制的基本知识。首先介绍了二次性能指标,然后讨论了调节器问题。
二次型简介二次型,quadratic form。n个变量的二次多项式称为二次型,即在一个多项式中,未知数的个数为任意多个,但每一项的次数都为2的多项式。线性代数的重要内容之一,它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的研究。二次型理论与域的特征有关。
二次型函数的定义定义设z是n维列向量,称标量函数

为二次型函数,并将P称为二次型的矩阵。上式是二次型函数的矩阵表达式,该式又可展开为
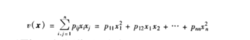
由式2可知,二次型函数v( x)实质上是关于xi和xj的二次多项式。由于多项式中,同类项合并后可再平分系数,因此可以整理成对称系数。也就是说,一个二次型函数总可以化成二次型矩阵P为实对称矩阵的二次型函数。1
线性控制理论简介线性控制理论是系统与控制理论中最为成熟和最为基础的一个组成分支,是现代控制理论的基石。
系统与控制理论的其他分支,都不同程度地受到线性控制理论的概念、方法和结果的影响和推动。
系统是由相互关联和相互作用的若干组成部分按一定规律组合而成的具有特定功能的整体。系统可具有完全不同的属性,如工程系统、生物系统、经济系统、社会系统等。但是,在系统理论中,常常抽去具体系统的物理或社会含义而把它抽象化为一个一般意义下的系统而加以研究,这种处理方法有助于揭示系统的一般特性。
系统最基本的特征是它的整体性,系统的行为和性能是由其整体所决定的,系统可以具有其组成部分所没有的功能,有着相同组成部分但它们的关联和作用关系不同的两个系统可呈现出很不相同的行为和功能。
理论研究对象线性系统理论的研究对象为线性系统,它是实际系统的一类理想化了的模型,通常可以用线性的微分方程和差分方程来描述。
在系统与控制理论中,我们将主要研究动态系统,通常也称其为动力学系统。动态系统常可用一组微分方程或差分方程来表征,并且可对系统的运动和各种性质给出严格和定量的数学描述。当描述动态系统的数学方程具有线性属性时,称相应的系统为线性系统。线性系统是一类最简单且研究得最多的动态系统。
线性二次型最优控制如果系统是线性的,性能指标泛函是状态变量和控制变量的二次型函数的积分,并且由状态变量构成线性状态反馈系统,则这样的最优控制称为线性二次最优控制。以下介绍的是线性二次型最优控制的基本知识。首先介绍了二次性能指标,然后讨论了调节器问题。2
二次型性能指标二次型性能指标的一般形式如下
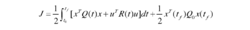
式中
Q(t)一一nxn维半正定的状态加权矩阵;
R(t)一一rxr维正定的控制加权矩阵;
Qo一一nxn维半正定的终端加权矩阵。
在工程实际中,Q(t)和R(t)常取对角阵。
下面对性能指标中各项的物理意义作逐一解析。
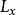
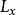 被积函数中第一项
被积函数中第一项 ,若x表示误差矢量,那么
,若x表示误差矢量,那么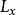 表示误差的平方。由此可见,是用以衡量误差x大小的代价函数,x越大,也就越大。Q(t)通常是对角线矩阵,对角线上的元素qii,分别表示相对应误差分量xi的重视程度,越加被重视的误差分量,希望它越小,相应地,其加权系数qii就应取得越大,如果对误差在动态过程中不同时刻有不同的强调时,那么,相应的qii就应取成时变的。
表示误差的平方。由此可见,是用以衡量误差x大小的代价函数,x越大,也就越大。Q(t)通常是对角线矩阵,对角线上的元素qii,分别表示相对应误差分量xi的重视程度,越加被重视的误差分量,希望它越小,相应地,其加权系数qii就应取得越大,如果对误差在动态过程中不同时刻有不同的强调时,那么,相应的qii就应取成时变的。
被积函数中第二项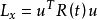 ,表示动态过程中对控制的约束或要求,如
,表示动态过程中对控制的约束或要求,如
果把u看成电压或电流的话,那么Lu与功率成正比,而
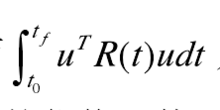
表示在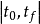 区间内消耗的能量,因此,Lu是衡量控制功率大小的代价函数。
区间内消耗的能量,因此,Lu是衡量控制功率大小的代价函数。
式中第二项突出了对终端误差的要求,叫做终端代价函数。例如在宇航的交会问题中,由于要求两个飞行体终态完全一致,因此,必须加上这一项,以体现tf时误差足够的小,至于Qo , R(t)的加权意义和Q(t)相仿。
如果最优控制的目的是使J →min,则其实际意义在于用不大的控制,来保持较小的误差,从而达到能量和误差综合指标的最优的目的。
状态调节器问题状态调节器的任务是,当系统状态由于任何原因偏离了平衡状态时,能在不消耗过多能量的情况下,保持系统状态各分量仍然接近于平衡状态。在研究这类问题时通常把初始状态矢量看成扰动,而把零状态取做平衡状态。于是调节器问题就变为寻找最优控制规律“,在有限的时间区间[fto } tf」内,将系统从初始状态转移到零点附近,并使给定的性能指标泛函取极值。
设线性时变系统的状态空间表述为
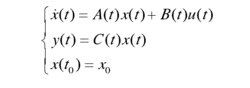
x, u, y一一分别为n, r, m维矢量;
A(t)一一hxh维系统矩阵;
B(t)一一hxr维输入矩阵;
C(t)一一mxh维输出矩阵;
性能指标泛函如上图所示
下面给出状态调节器的解最优控制器为
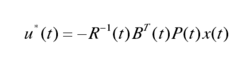
最优性能指标为
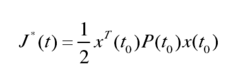
式中P(t)满足下面的Riccati矩阵微分方程
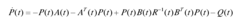
边界条件
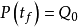




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国