[科普中国]-准线性系统

准线性系统（quasi linear system）是指在实际问题中所建立的非线性系统模型应该能够在一定的条件下线性化使得解决问题的方法简单化而不致超过允许误差的系统模型 。

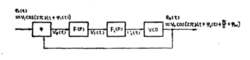
严格地说，锁相环是一个非线性系统，但是当环路锁定以后，在一定的动态范围内，系统又可以认为是线性的。这种系统称为线性化系统或准线性系统。它和严格的线性系统有共性，但也有本质的区别。弄清这些区别，可使我们对环路有一个更加清楚而明确的认识为此先将图1的锁相环重新画出如图2所示。

在图2中，所标明的信号(如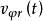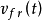，等)均为实际信号，因此其下标加有符号 r 。这些信号又可写成如下形式：

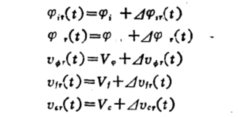
其中，φ为固定相位；V 均为直流电压。它们都是常数。这些常数决定了环路中各部件的工作点(如鉴相器的工作点。均为增量信号，它们使工作点摆动。在一个系统中，若所有的信号之间都存在线性关系，则称为线性系统。例如，由线性电感、电容、电阻组成的电路即属于此类。若系统中各个实际信号之间虽不存在线性关系，但是当各个部件的工作点固定以后，在一定的范围内，所有增量信号之间却存在线性关系，则这种系统称为准线性系统。例如，线性放大器、线性鉴相器，锁相环等就属于这一类。

线性系统是一数学模型，是指用线性运算子组成的系统。相较于非线性系统，线性系统的特性比较简单。线性系统需满足线性的特性，若线性系统还满足非时变性（即系统的输入信号若延迟τ秒，那么得到的输出除了这τ秒延时以外是完全相同的），则称为线性时不变系统。1

一个系统,如果其输出不与其输入成正比，则它是非线性的。从数学上看，非线性系统的特征是叠加原理不再成立。叠加原理是指描述系统的方程的两个解之和仍为其解。叠加原理可以通过两种方式失效。其一，方程本身是非线性的。其二,方程本身虽然是线性的,但边界是未知的或运动的。

“线性”与“非线性”是两个数学名词。所谓“线性”是指两个量之间所存在的正比关系。若在直角坐标系上画出来，则是一条直线。由线性函数关系描述的系统叫线性系统。在线性系统中，部分之和等于整体。描述线性系统的方程遵从叠加原理，即方程的不同解加起来仍然是原方程的解。这是线性系统最本质的特征之一。“非线性”是指两个量之间的关系不是“直线”关系，在直角坐标系中呈一条曲线。最简单的非线性函数是一元二次方程即抛物线方程。简单地说，一切不是一次的函数关系，如一切高于一次方的多项式函数关系，都是非线性的。由非线性函数关系描述的系统称为非线性系统。

定性地说，线性关系只有一种，而非线性关系则千变万化，不胜枚举。线性是非线性的特例，它是简单的比例关系，各部分的贡献是相互独立的；而非线性是对这种简单关系的偏离，各部分之间彼此影响，发生耦合作用，这是产生非线性问题的复杂性和多样性的根本原因。正因为如此，非线性系统中各种因素的独立性就丧失了：整体不等于部分之和，叠加原理失效，非线性方程的两个解之和不再是原方程的解。因此，对于非线性问题只能具体问题具体分析。

线性与非线性现象的区别一般还有以下特征：

（1）在运动形式上，线性现象一般表现为时空中的平滑运动，并可用性能良好的函数关系表示，而非线性现象则表现为从规则运动向不规则运动的转化和跃变；

（2）线性系统对外界影响的响应平缓、光滑，而非线性系统中参数的极微小变动，在一些关节点上，可以引起系统运动形式的定性改变。在自然界和人类社会中大量存在的相互作用都是非线性的，线性作用只不过是非线性作用在一定条件下的近似。

我们知道，在许多实际问题中所建立的方程系统往往是非线性的，它要比线性情况复杂的多，这就使我们设想所要研究的问题能否线性化为了达到这个目的，首先必须经过理想化，略去某些次要因素，使得线性化的结果仍能真实的反映原问题的本质。然而，并非每个问题都可如此线性化而且，由于初始值一般通过测量取得，不可避免会产生一定的误差，这就要求当初始值有微小变化时，其解的变化也应任意小。2

对于非线性系统

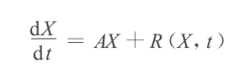
其中：A为系统线性部分的系数矩阵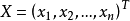；为系统变量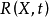；为非线性项。我们假设它满足以下条件：

(1) 初始条件；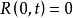

(2)极限条件

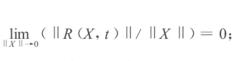
(3)相当于（*）的线性系统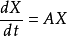的特征方程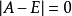不具有零实部根，且其根都具有负实部时，我们称系数矩阵A是稳定矩阵。当其根至少有一个具有正实部时，则称A为不稳定矩阵，满足这样条件的非线性系统(*)这就是我们要研究的准线性系统。

对于系统(*)的系数矩阵A为稳定的充要条件是：对任意给定的正定实对称矩阵Q，存在唯一正定实对称矩阵P，使等式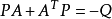成立。

如果A是稳定矩阵，则系统(*)的零解是渐稳的；如果A是不稳矩阵;则(*)的零解是不稳的。

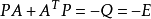设系数矩阵A是稳定矩阵，则由上引理，对于给定的实对称单位正定矩阵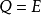，一定存在唯一的正定实对称矩阵P，使得成立，我们构造函数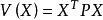，则V(X)为定正函数，下面求经过系统(*)的全导数：

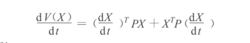
将系统(*)代入此，得到

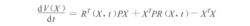
由于系统(*)是准线性系统，则准线性项R (X, t )满足极限条件

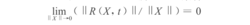
说明当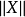很小时，R (X, t)是X 的高阶无穷小，即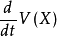的符号可由它的右端项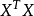来确定，显然

定负函数。

根据李亚普诺夫基本定理，故知系统(*)的零解是渐稳的.

至于不稳定性的证明，可以从相应非线性系统(*)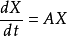的解的结构中加以考虑。

应该指出，对于一般非线性系统(*)，若接照其系数矩阵A的特征根的符号来分类，还有下面一种情况，就是A的全部特征根中没有正的实部但却有零实部，这种情况就是所谓的临界情形。李亚普诺夫定理已经证明：在这种情形下，可以适当的分别选取函数R (X, t )，使(*)的零解X= 0既可能是稳定的，又可能是不稳定的。

可以看出，对于准线性系统的稳定性问题，关键就在于判断系数矩阵A是否稳定，即A的特征根的符号决定着系统的稳定性态。然而，当A的阶数较高时，欲想求出它的全部特征根往往是很困难的，甚至求不出来。实际上，我们所关心的不是特征值，而只是其符号。为此，我们用霍尔维兹(Hmwitz )代数法则来解决这个问题。

(Hmwitz法则)首项系数为1的实系数多项式方程

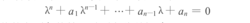
的全部根的实部为负值的充要条件是n阶霍尔维兹矩阵:

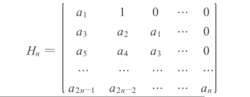
的全部主子式为正值，其中当i> n时，ai=0.

根据稳定矩阵的定义和定理1的结论，可将定理2改述为:

设准线性系统(*)的特征方程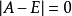。有以下形式:

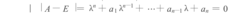
则系统(*)的零解X=0渐稳的充要条件是((1)的所有各阶霍尔维兹行列式:

均大于零(当i > n时，ai = 0)可见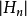，可用条件an代替。

事实上，如果各行列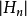均大于零((k =1，2,…，n-1)，

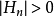则可由推出an>0。