[科普中国]-非线性PI控制

在生产生活的各个领域中许多系统都存在着或多或少的不确定因素，然而为了简化控制器设计的复杂程度，往往在对这些系统进行建模的过程中忽略了这些不确定的因素，因此系统的动态性能要受到一定程度的影响，甚至有时会出现不稳定的情况。例如在对飞机进行控制器的设计时，飞机在飞行的过程中会受到风速，气压，温度等很多不确定因素的影响，而这些因素如果不被考虑到控制器的设计中，很有可能引起飞行的失败，造成生命和财产的损失。因此自动控制技术面临一个很重要的课题，即在被控对象含有某种不确定性的前提下，如何设计控制器使系统尽可能接近或者达到理想的控制指标。上述问题就是通常所说的鲁棒控制问题，随着控制理论的发展，非线性PI控制也属于鲁棒控制的一种。

随着非线性控制理论研究的深入，非线性不确定系统的控制成为目前控制界的研究热点之一。非线性PI控制是一种新型的控制方法，它摒弃了传统自适应控制采用的参数辨识加反馈控制器设计的结构，将系统的动态表达成期望动态特性加扰动项的形式，在不知道非线性不确定函数具体形式的情况下，通过确定该函数的界来设计控制器的参数，使系统能够达到期望动态特性。

非线性PI控制方法是一种适用于控制线性系统和非线性系统的方法，尤其适用于对不确定系统进行控制，与自适应控制方法的不同之处在于该方法不需要对未知的参数进行辨识。在对包含非线性不确定项的系统进行控制时，如果采用自适应控制算法，必须对非线性参数化的未知项进行辨识，然后根据确定性等效原理和李亚普诺夫稳定性理论推出控制器。然而目前对非线性参数化的未知项进行辨识是比较困难的，大多数方法都是建立在对非线性函数特性的某些几何假设的基础上，并不能广泛应用。如果利用反馈线性化或其他方法将该非线性不确定项转化成为线性参数化的形式，将可能导致由于超参数化造成的系统阶数的增加和不稳定的零极点对消等消极因素。非线性PI控制方法弥补了自适应控制在这方面的不足，它首先将系统表达成期望动态特性加扰动项的形式，通过了解非线性不确定项的界来设计非线性PI控制器参数，在控制器的作用下随着扰动项渐近趋于零，使系统能够渐近达到期望的动态特性，从而实现控制目的1。

首先给出非线性PI控制器的定义：对于可测信号 ，参考信号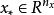 和标量控制信号，定

义如下三个映射：

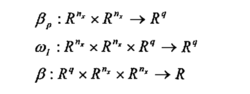
通过下面的式子可以构成非线性PI控制器

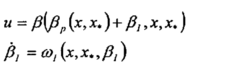
式中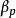， 和 别为非线性比例系数和微分系数。

事实上，从上面的定义可以立即推出下面的结论：经典的单输入单输出线性PI控制器是非线性PI控制器的特例，下图为单输入单输出线性PI控制器

采用一个简单的例子说明非线性PI控制器的设计原理。假设需要控制的对象为包含有界非线性不确定项的一阶系统：

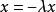式中x表示系统状态，u表示控制输入，a为已知参数， 为关于x的非线性函数，其参数和具体形式不知道，只知道它的界。控制目标是设计控制输入u，使得 。为了实现控制目标，设期望动态特性为量 ，可以看出，如果系统能够达到期望动态特性，则状态x可以指数收敛到零。

系统表达成期望动态特性加扰动项的形式：

若存在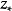 ，使得对于每一个x值，扰动项：

并且 渐近收敛于z，则系统能够渐近达到期望的动态特性。为此，考察z的动态特性：

为了使扰动项的根能够成为z的平衡点，选择：

可以得到：

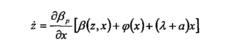
所以得出结论：如果z存在稳定的平衡点，则扰动项能够渐近趋于零。为了考察z是否存在稳定的平衡点，将z的动态特性看成关于z的系统，将x视为参数，并且定义 ，选择：

可以证明，对于所有的x，存在充分大的正整数N，有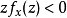：。在该控制器的作用下，系统能够在有限的时间内收敛到该区域。

自适应控制是也是一种控制方法，对于通常形式的，当用非线性参数化逼近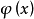时，自适应控制是无能为力的；当使用线性参数化逼近时，为了保证逼近的精度，就必须增加未知参数的个数，从而导致系统实际维数的增加，影响了系统的动态性能。

而非线性PI控制方法不需要对未知的非线性函数进行参数化，实际上也避免了参数估计问题，它通过设计非线性PI控制器及其参数，调解系统逐渐达到期望的动态特性，是解决这类问题的比较好的方法。